이 게시글에서는 SLAM에서의 KF와 EKF를 기준으로 설명할 예정입니다.
Kalman Filter란?
칼만 필터는 현재 상태(state) $\mu$와 공분산(covariance) $\Sigma$를 기반으로 다음 상태를 추정하는 방법입니다. $\mu$와 $\Sigma$만으로 나타낼 수 있는 Gaussian 분포를 따르며, 지난 게시글의 Bayesian Filter와도 관계가 있습니다. 선형 칼만 필터를 설명하기 전에 가우시안 분포에 대해서 조금 설명하도록 하겠습니다.
Gaussian 분포
$p(x)=\frac{1}{ \sqrt{2 \sigma^2 \pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$
$p(x)=\frac{1}{ \sqrt{det(2\pi\Sigma)}}e^{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)}$
가우시안 분포는 단일 변수(single variable)과 다변수(multi variable)의 표현 방식이 있으며, SLAM 에서는 로봇의 현재 state를 벡터 $(x,y,\phi)$로 표시하기 때문에 다변수 가우시안 분포를 사용하는 것이 좋습니다.
선형 모델의 가우시안 분포
일반적으로, 선형 모델은 다음과 같이 표현할 수 있습니다.
$Y=AX+B$
이때, $X$가 가우시안 분포를 따른다고 할 때, 확률은 다음과 같이 나타낼 수 있습니다.
$X \sim N(\mu_x, \Sigma_x)$
선형 변환 후의 확률변수 $Y$의 분포는 다음과 같습니다.
$Y \sim N(A\mu_x+B, A\Sigma_xA^T)$
유도과정
$X$의 평균인 $\mu_x$의 선형변환 $\mu_y$는 직관적으로 이해되지만, 공분산 $\Sigma_y$는 조금 의문이 남습니다. 유도과정을 간단히 정리하겠습니다.
$\begin{align*} \mu_y &= E((y-\mu_y)(y-\mu_y)^T) \\
&= E((y-(A\mu_{x}+B))(y-(A\mu_{x}+B))^T) \\
&= E(((AX+B)-(A\mu_{x}+B))((AX+B)-(A\mu_{x}+B))^T) \\
&= E(\left [ A(X-\mu_x) \right ] \left [ A(X-\mu_x) \right ]^T) \\
&= E( A(X-\mu_x)(X-\mu_x)^{T} A^T) \\
&= AE((X-\mu_x)(X-\mu_x)^T)A^T \\
&= A \Sigma_x A^T
\end{align*}$
선형 Kalman Filter
선형 칼만 필터는 motion model과 observation model을 선형으로 가정합니다.
motion model: $x_t = A_tx_{t-1}+B_tu_t+\epsilon_t$
observation model: $z_t = H_tx_t+\delta_t$
- $A_t$: control input $u_t$와 노이즈($\epsilon_t$)가 없을 때의 t-1과 t의 state 사이의 관계, n*n matrix
- $B_t$: control input $u_t$가 다음 state $x_t$에 어떤 영향을 미치는지를 나타낸 matrix, n*l matrix
- $H_t$: 현재 로봇의 상태를 나타내는 state $x_t$와 센서의 관측 정보(observation)의 관계, k*n matrix
- $\epsilon_t,\;\delta_t$: 평균이 0이며 공분산이 각각 $R_t,\;Q_t$인 확률변수, 가우시안 표준정규분포를 따름.
따라서 이를 가우시안 분포 공식에 적용하면, Bayesian Filter의 motion model과 observation model 확률을 구할 수 있습니다.
- Motion model
$p(x_t|u_t,x_{t-1})=\frac{1}{ \sqrt{det(2\pi R_t)}}e^{-\frac{1}{2}(x-A_tx_{t-1}-B_tu_t)^TR_t^{-1}(x-A_tx_{t-1}-B_tu_t)}$
$p(z_t|x_t)=\frac{1}{ \sqrt{det(2\pi Q_t)}}e^{-\frac{1}{2}(x-H_tx_t)^TR_t^{-1}(x-H_tx_t)}$
Motion model은 prediction step에서, Observation model은 correction step에 적용됩니다.
$\overline{bel}(x_t)=\int_{x_{t-1}}p(x_t|u_t,x_{t-1})bel(x_{t-1})dx_{t-1}$
$bel(x_t) = \eta p(z_t|x_t)\overline{bel}(x_t)$
t에서의 state 확률 $\overline{bel}(x_t)$은 motion model에 의해 결정되고(prediction step), prediction step에서 계산된 t에서의 state 확률 $\overline{bel}(x_t)$은 observation model에 의해서 보정됩니다.
이때, 모든 확률 분포를 Gaussian 확률 분포를 따른다고 가정하는 모델이 바로 Kalman Filter입니다. Gaussian 분포를 따른다고 가정하면 간단히 평균 $\mu$과 분산(공분산) $\sigma(\Sigma)$로 표시하기 때문에 두개의 파라미터만으로 확률분포를 표현할 수 있는 장점이 있습니다. Kalman Filter 알고리즘은 다음과 같습니다.
$\begin{align*} 1&: Kalman Filter(\mu_{t-1}, \Sigma_{t-1}, u_t, z_t) \\
& [Prediction\;step] \\
2&: \overline{\mu}_t=A_t\mu_{t-1}+B_tu_t \\
3&: \overline{\Sigma}_t=A_t\Sigma_{t-1}A_t^T+R_t \\
& [Correction\;step] \\
4&: K_t=\overline{\Sigma}_tH_t^T(H_t\overline{\Sigma}_tH_t^T+Q_t)^{-1}\\
5&: \mu_t = \overline{\mu}_t+K_t(z_t-H_t\mu_t) \\
6&: \Sigma_t = (I-K_tH_t)\overline{\Sigma}_t \\
7&: return\;\mu_t, \Sigma_t
\end{align*}$
Kalman Filter는 Bayesian Filter이기 때문에 predicton step과 correction step을 갖고 있습니다. 각 단계에 대해 Kalman Filter 알고리즘을 관찰해 봅시다.
$\begin{align*} 1&: Kalman Filter(\mu_{t-1}, \Sigma_{t-1}, u_t, z_t) \\
& [Prediction\;step] \\
2&: \overline{\mu}_t=A_t\mu_{t-1}+B_tu_t \\
3&: \overline{\Sigma}_t=A_t\Sigma_{t-1}A_t^T+R_t
\end{align*}$
prediction step은 다음 state를 motion model을 통해 예측하는 단계입니다. 계속 똑같은 말을 반복하는거 같긴 하지만, 우선 알아보도록 합시다. 이전 state와 motion $u_t$의 결합을 통해 다음 단계의 평균을 추측합니다. 하지만 이때는 아직 완전히 정확하지 않은 상태이므로 준 현재 state라는 의미로 평균과 공분산 기호 위에 작대기를 그어 표현해 줍니다. 다음 correction 단계에서 추가적인 과정을 통해 더 정확한 위치를 잡을 것입니다.
이때 $R_t$는 process noise로, control inpud $u_t$의 공분산 $M_t$에서 선형 변환을 한번 더 거친 형태의 공분산입니다. 그 형태는 다음과 같습니다.
$R_t=B_tM_tB_t^T$
일반적으로 모바일 로봇에서 control input은 wheel encoder로부터 구해진 odometry가 들어가고, encoder에 대한 uncertainty가 공분산 $M_t$가 됩니다.
$\begin{align*}
& [Correction\;step] \\
4&: K_t=\overline{\Sigma}_tH_t^T(H_t\overline{\Sigma}_tH_t^T+Q_t)^{-1}\\
5&: \mu_t = \overline{\mu}_t+K_t(z_t-H_t\mu_t) \\
6&: \Sigma_t = (I-K_tH_t)\overline{\Sigma}_t \\
7&: return\;\mu_t, \Sigma_t
\end{align*}$
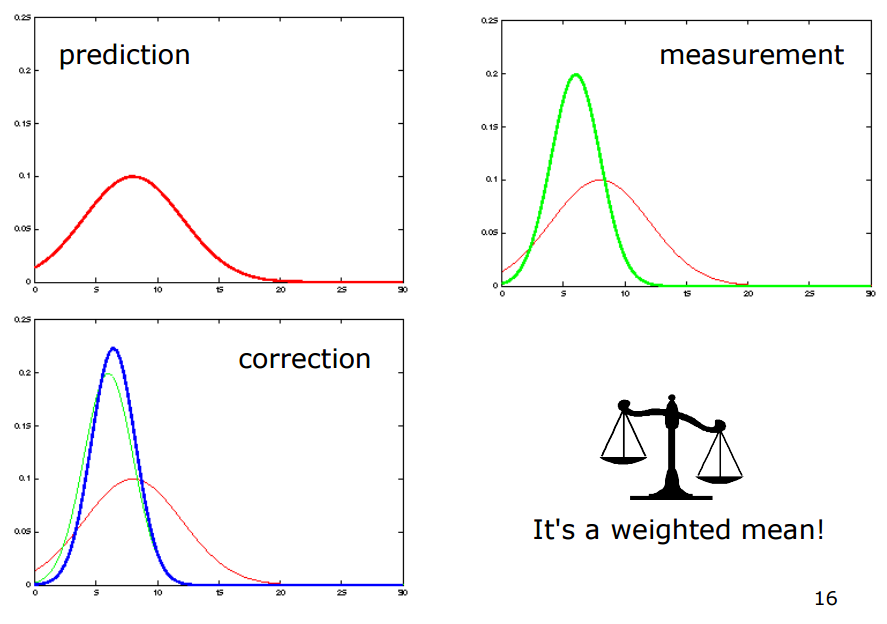
Correction 단계는 칼만 게인을 구하여 조금 부정확했던 현재 state $\overline{\mu}_t$를 보정해 주는 과정입니다. 칼만 게인 $K_t$는 현재 예측값 $\overline{\mu}_t$와 관측을 통해 예측한 값 $z_t-H_tx_t$ 중 어떤 것을 더 많이 보정에 반영할지, 즉 센서를 더 믿을 것인가, 기댓값을 더 믿을 것인가를 조절해 주는 가중치입니다.
예를 들어 observation 공분산 $Q_t$가 무한대의 값을 가지는 대각행렬이라고 하면 observation의 uncertainty가 무한대, 즉 센서 관측값을 전혀 못 믿겠다는 의미가 됩니다. 그렇다면, 칼만 게인의 분모값(다변수 일때는 역행렬값)이 무한대가 되고, 칼만 게인 값은 0에 수렴할 것입니다. 그 결과, 최종 평균은 $\mu_t=\overline{\mu}_t$이 됩니다. 반대로 $Q_t$의 값이 0의 대각행렬이라면 칼만 게인은 $K_t=C_t^{-1}$이 되고, 최종 평균은 $\mu_t=H_t^{-1}z_t$이 됩니다.
결국 예측 평균과 관측을 통한 예측 평균을 저울질하여 더 실제와 가까운 쪽으로 잘 섞어 주는 과정입니다.
EKF (Extended Kalman Filter)
확장 칼만 필터(Extended Kalman Filter)는 칼만 필터를 비선형 모델에 적용할 수 있도록 한 방식입니다. 지금까지 다뤘던 motion model과 observation model은 선형이었지만, 일반적으로 선형보다 비선형 모델이 더 많기 때문에 EKF를 사용합니다. 비선형 모델을 적용한 motion model과 observation model은 다음과 같습니다.
$x_t=g(u_t, x_{t-1})+\epsilon_t$
$z_t=h(x_t)+\delta_t$
하지만 이 모델을 그대로 칼만 필터에 적용할 경우 아래 이미지와 같은 문제가 발생합니다.
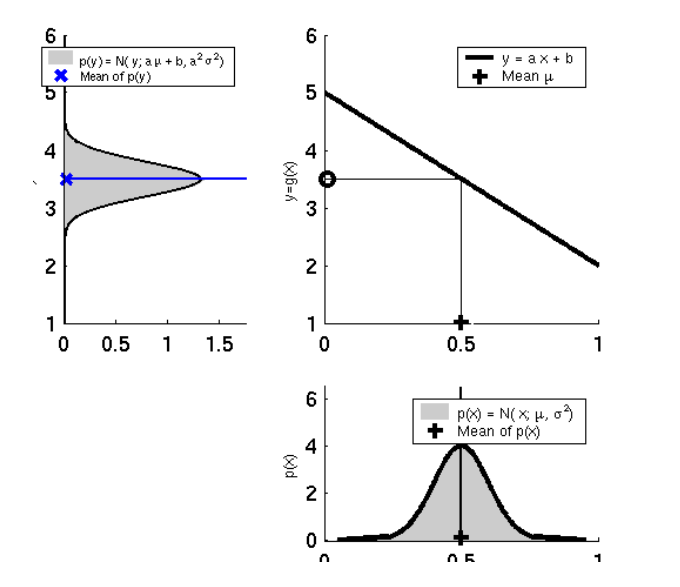
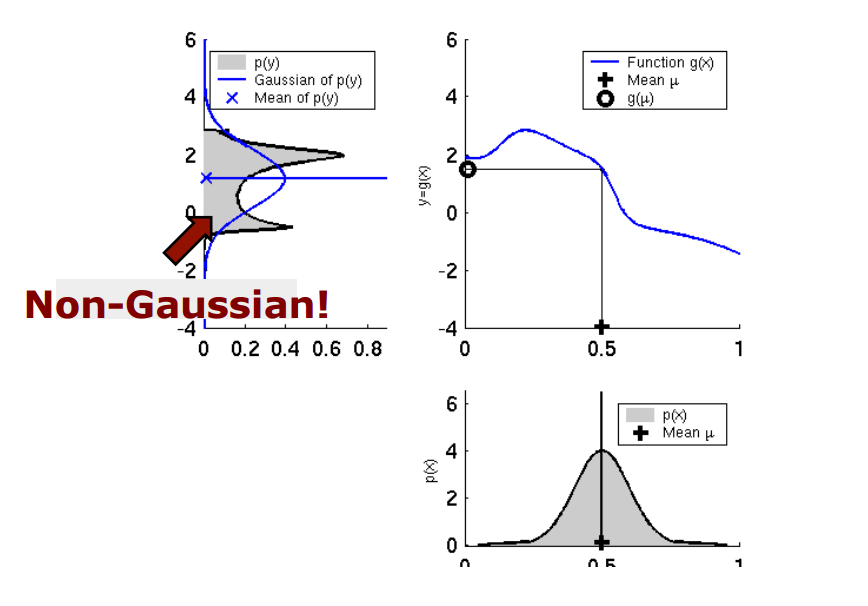
왼쪽 이미지처럼 선형 모델에선 입력이 가우시안 분포를 따른다면 선형성에 의해서 출력도 가우시안 분포를 따릅니다. 하지만 비선형 모델에서는 입력이 가우시안 분포를 따른다고 해도, 출력은 가우시안 분포를 따르지 않는 문제가 발생합니다. 이런 점을 해결하기 위해서 비선형 함수의 선형화(Linearization) 시키는 과정이 필요합니다.
선형화(Linearization)
EKF에서 비선형 함수를 선형화 시키기 위해서 1차 Taylor 근사법을 사용하는데, 선형 근사화된 모델은 다음과 같습니다.
$g(u_t,x_{t-1})\approx g(u_t, \mu_{t-1})+\frac{\partial g(u_t, \mu_{t-1})}{\partial x_{t-1}}(x_{t-1}-\mu_{t-1})$
$h(x_t)\approx h(\overline{\mu}_t)+\frac{\partial h(\overline{\mu}_t)}{\partial x_t}(x_t-\overline{\mu}_t)$
이때 비선형 함수를 state $x_t$로 편미분하여 matrix를 생성하는데 이 행렬을 Jacobian이라고 합니다. 두 matrix는 $G_t=\frac{\partial g(u_t, \mu_{t-1})}{\partial x_{t-1}}$과 $H_t=\frac{\partial h(\overline{\mu}_t)}{\partial x_t}$로 표기합니다.
아래 그림은 Talyer 근사화를 통해 선형화를 하였을 때의 특징을 보여줍니다.
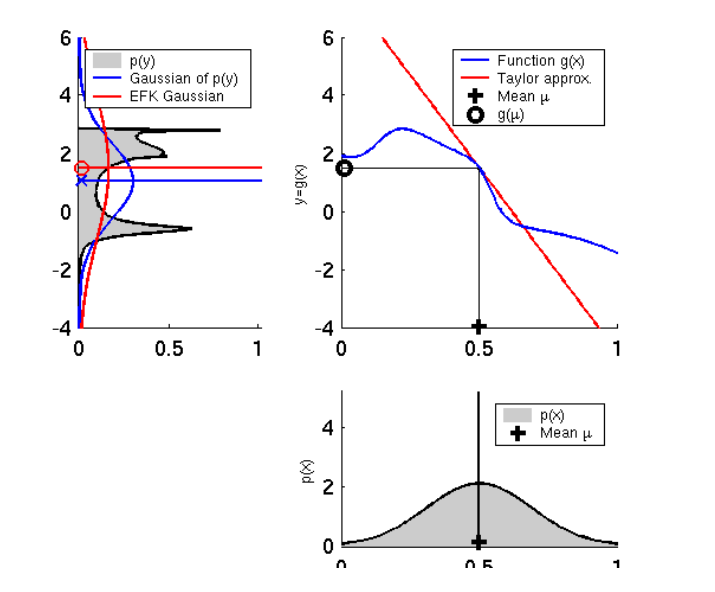
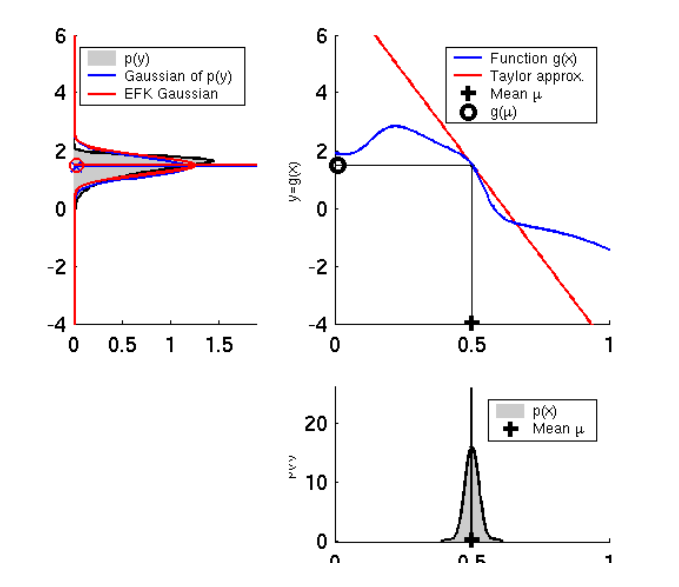
왼쪽 그림은 입력의 분산(다변수에서는 공분산)이 클 때 평균이 실제값과 크게 차이나는 결과를 볼 수 있습니다. 오른쪽 그림은 입력의 분산이 작을 때 평균이 실제값과 차이가 작은 것을 볼 수 있습니다.
EKF algorithm
선형화된 motion 모델과 observation 모델을 이용한 bayes filter는 다음과 같습니다.
- linearized prediction model
$p(x_t|u_t,x_{t-1}) \approx \frac{1}{ \sqrt{det(2\pi R_t)}}e^{-\frac{1}{2}(x_{t}-g(u_t,x_{t-1}))^T R_{t}^{-1}(x_t-g(u_t,x_{t-1}))}$
- linearized correction model
$p(z_t|x_t) \approx \frac{1}{ \sqrt{det(2\pi Q_t)}}e^{-\frac{1}{2}(x_{t}-h(\overline{\mu}_t))^T Q_{t}^{-1}(x_t-h(\overline{\mu}_t))}$
Kalman Filter와 마찬가지로 $R_t$, $Q_t$는 process noise, measurement noise입니다. EKF 알고리즘은 다음과 같습니다.
$\begin{align*} 1&: Extended\;Kalman\;Filter(\mu_{t-1}, \Sigma_{t-1}, u_t, z_t) \\
& [Prediction\;step] \\
2&: \overline{\mu}_t=g(u_t, \mu_{t-1}) \\
3&: \overline{\Sigma}_t=G_t\Sigma_{t-1}G_t^T+R_t \\
& [Correction\;step] \\
4&: K_t=\overline{\Sigma}_tH_t^T(H_t\overline{\Sigma}_tH_t^T+Q_t)^{-1}\\
5&: \mu_t = \overline{\mu}_t+K_t(z_t-h(\overline{\mu}_t)) \\
6&: \Sigma_t = (I-K_tH_t)\overline{\Sigma}_t \\
7&: return\;\mu_t, \Sigma_t
\end{align*}$
EKF 알고리즘과 KF 알고리즘의 차이는 무엇보다 비선형 함수의 선형화입니다. KF의 3,4번 식의 $A_t$ 행렬은 EKF에서 $G_t$ 행렬로, $H_t$ 행렬은 $h(\overline{\mu}t)$ 함수의 자코비안 행렬 $H_t$로 대체되었습니다. 여기서 $R_t$는 process noise이며, control input의 공분산 행렬이 $M_t$일 때 $R_t=V_tM_tV{t}^T$입니다. 여기서 $V_t$는 $g(u_t, \mu_{t-1})$를 control input인 $u_t$로 편미분한 자코비안입니다.
참고 사이트
Jinyoung - [SLAM] Kalman filter and EKF(Extended Kalman Filter)
Refstop
Deep Learning 및 SLAM을 공부하고 있습니다.







Comments