Localization이란 무엇?
Localization은 자율주행차 또는 모바일 로봇이 자신의 위치를 인지하는 것을 의미합니다. 직역하면 위치 추정입니다. 어떻게 하면 자동차가 자기 위치를 인식 할 수 있을까요? 그것은 바로 센서와 지도를 이용하는 것입니다. 아직은 SLAM이 아닌 지도를 알고 움직이는 자동차로 생각합니다. 이 작업에서 가장 중요한 것은 확률, $bel(x_t)$입니다.
자율주행차의 확률 $bel(x_t)$

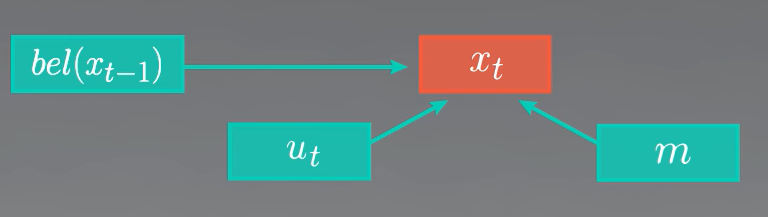
자동차는 확률을 $bel(x_t)$라는 확률함수의 형태로 표현합니다. $x_t$는 자동차의 상태를 의미하는데, 이 강의에서는 position으로 취급합니다. 따라서 $bel(x_t)$는 자동차가 $x_t$라는 지점에 있을 확률이라고 해석할 수 있습니다. 이를 확률함수의 형태로 표현하면 그림과 같이 $bel(x_t)=p(x_t|z_{1:t}, u_{1:t}, m)$이 됩니다. 확률함수의 조건인 $z_{1:t}, u_{1:t}, m$에 대해서 알아보도록 하겠습니다.
1. $z_{1:t}$: Observation
$z_{1:t}$는 자동차의 관측(Observation)과 관련된 항입니다. 시간 1부터 $t$까지의 관측값을 반영한 성분입니다. 앞으로 들 예시에서는 자동차의 position으로부터 landmark까지의 거리로 생각합니다. 또한, 이 항을 확률함수로 나타낸다면 $p(z_t)$로 나타냅니다. 의미는 실제 관측값과 자동차가 생각하는 관측값의 차이를 정규분포에 따라 도출해낸 확률, 즉 자동차가 생각하는 관측값이 맞을 확률입니다.
2. $u_{1:t}$: Motion
$u_{1:t}$는 자동차의 움직임(Motion)과 관련된 항입니다. 자동차의 움직임은 역시 바퀴가 굴러가는 이동입니다. 앞으로 들 예시에서 역시 자동차가 이동한 거리로 생각합니다.
3. $m$: Map
$m$은 단순한 지도입니다. landmark의 좌표를 나타내는 항이라고 볼 수 있습니다. 예시 역시 별 차이 없이 landmark의 위치를 담고 있는 값으로 생각합니다.
4. $x_t$: Position
$x_t$는 자동차가 있는 위치(Position)와 관련된 항입니다. 자동차가 생각하는 위치라고 볼 수 있습니다. 실제 값과는 다를 수 있습니다.
결론
결국, 여기서 구하고자 하는 값은 $p(x_t)$입니다. 이는 자동차가 알고 있는 자신의 위치가 맞을 확률을 나타내는 확률함수입니다. 그럼 그림의 확률함수를 한번 봅시다.
$\large{
bel(x_t)=p(x_t|z_{1:t}, u_{1:t}, m)
}$
그림의 확률함수는 결국 조건부 확률입니다. $1:t$ 동안의 관측값 $z$, 이동값 $u$, 지도 $m$이라는 조건일 때, 시간 $t$일 때 자동차가 위치 $x$에 있는게 맞을 확률을 의미합니다.
NOTE!
SLAM에서의 확률 $bel(x_t)$는 조금 다릅니다. 위치추정과 맵핑을 동시에 수행하기 때문에 지도 $m$ 역시 계속 업데이트 해 주어야 하는 항목입니다. 따라서 SLAM에서의 $bel(x_t)$는 $p(x_t, m|z_{1:t}, u_{1:t})$이 됩니다. 하지만 아직은 SLAM에서의 $bel(x_t)$는 신경쓰지 않습니다.
베이즈 정리
베이즈 정리는 지난번에 작성한 게시글이 있지만 간단히 다시 한번 설명하겠습니다. 베이즈 정리의 생김새는 다음과 같습니다.
$\large{
P(A|B)=\frac{P(B|A)P(A)}{P(B)}
}$
이 정리에서 주목해야 할 부분은 사전확률(Prior) $P(A)$와 사후확률(Posterior) $P(A|B)$입니다. 베이즈 정리의 핵심 기능은 사건이 발생하기 이전의 사건 발생 확률과 발생했을 때의 조건을 조합하여 사후확률, 즉 사건 발생 이후의 사건 발생 확률을 도출하는 것입니다. 이는 베이즈 정리를 여러번 사용하여 확률을 계속 업데이트하는 형태로 많이 사용됩니다. 사건과 발생이란 말이 너무 많으니 게슈탈트 붕괴가 오네요…. 심플하게 표현하면 사전+조건=사후로 정리할 수 있습니다. +는 더하기가 아닌 조합한다는 의미입니다.
Localization + 베이즈 정리
이제 Markov Localization 공식 유도의 첫번째 단계입니다. 우리는 베이즈 정리와 다른 정리들을 사용하여 확률함수 $p(x_t|z_{1:t}, u_{1:t}, m)$을 재귀 형태로 만들 것입니다.
1. 베이즈 정리로 $bel(x_t)$ 나타내기
우선 확률함수 $p(x_t|z_{1:t}, u_{1:t}, m)$을 베이즈 정리에 따라 나타내 봅시다. $z_{1:t}$를 $z_t$와 $z_{1:t-1}$으로 분리합니다. 이때 분리한 $z_t$는 위의 베이즈 정리에서 사건 $B$를 맡을 것입니다.
$\large{
bel(x_t)=p(x_t|z_{1:t}, u_{1:t}, m)=p(x_t|z_t, z_{1:t-1}, u_{1:t}, m)
}$
그 다음 베이즈 정리를 사용합니다. 사건 $A$는 당연히 $x_t$입니다.
$\large{
p(x_t|z_t, z_{1:t-1}, u_{1:t}, m)=\frac{p(z_t|x_t, z_{1:t-1}, u_{1:t}, m)p(x_t|z_{1:t-1}, u_{1:t}, m)}{p(z_t|z_{1:t-1}, u_{1:t}, m)}
}$
굉장히 길고 복잡한 식이 되었습니다. 조금 더 정리해 봅시다.
2. Normalizer 처리
베이즈 정리에서 분모는 Normalizer로서 생략 또는 상수화 시킬 수 있습니다. 여기서 Normalize는 정규화라고 하는데, 가장 일반적인 항으로 만드는 것을 의미합니다.
간단한 예를 들어보겠습니다. 어떤 날 비가 올 확률이 항상 0.6인 세계가 있고, 이 세계는 비 또는 맑은 날씨밖에 없고, 하루하루가 독립시행이라고 가정합니다. 이때 어떤 날 비가 왔을때, 다음날도 비가 올 확률과 다음날엔 맑은 확률을 구해 봅시다.
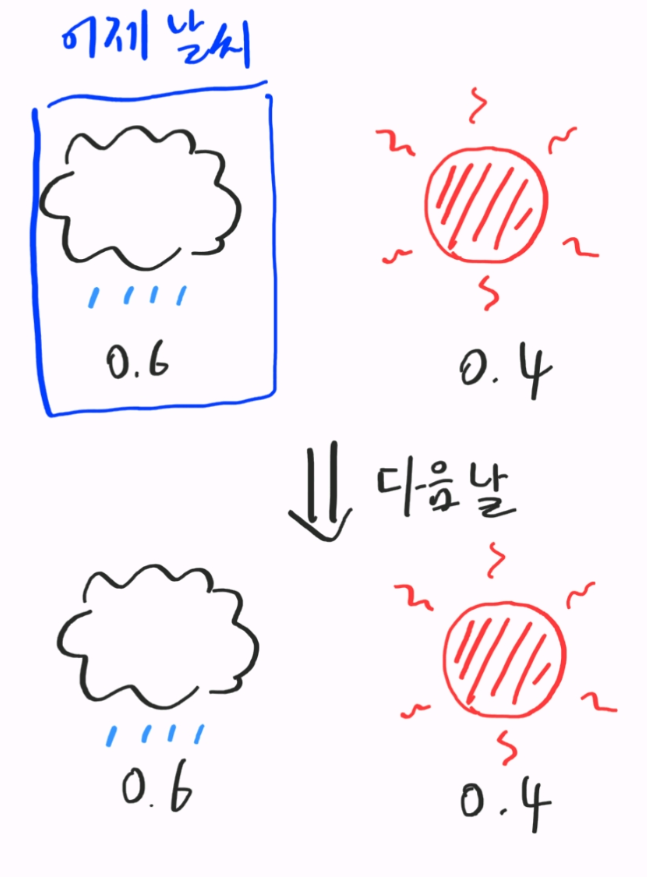
먼저 이틀간의 날씨가 비-비 일 확률입니다. 0.6$\times$0.6=0.36입니다. 그 다음으로 비-맑음일 확률은 0.6$\times$0.4=0.24입니다. 이 두 확률의 합은 0.6입니다.

이때 확률의 총합을 1로 만들고 싶다면, 어제의 날씨가 비였을 확률로 이들을 나눠 줍니다.
$\large{
\frac{0.36}{0.6}+\frac{0.24}{0.6}=1
}$
이런식으로 일반적인 항으로 만들어 주는 것을 정규화라고 합니다. 다시 자동차의 확률함수 식으로 돌아가 봅시다. 이 식에서의 normalizer 항은 다음과 같습니다.
$\large{
\begin{align*}
p(x_t|z_t, z_{1:t-1}, u_{1:t}, m) &= \frac{p(z_t|x_t, z_{1:t-1}, u_{1:t}, m)p(x_t|z_{1:t-1}, u_{1:t}, m)}{p(z_t|z_{1:t-1}, u_{1:t}, m)} \\
&= \underbrace{\frac{1}{p(z_t|z_{1:t-1}, u_{1:t}, m)}}_{\text{Normalizer}}p(z_t|x_t, z_{1:t-1}, u_{1:t}, m)p(x_t|z_{1:t-1}, u_{1:t}, m)
\end{align*}
}$
표시된 항을 정규화 상수로 취급하고, $\eta$로 표현합니다. 이를 다시 정리하면 다음과 같습니다.
$\large{
p(x_t|z_t, z_{1:t-1}, u_{1:t}, m) = \eta \; p(z_t|x_t, z_{1:t-1}, u_{1:t}, m)p(x_t|z_{1:t-1}, u_{1:t}, m)
}$
Motion 모델과 Observation 모델
$\large{
p(x_t|z_t, z_{1:t-1}, u_{1:t}, m) = \eta \; \underbrace{p(z_t|x_t, z_{1:t-1}, u_{1:t}, m)}_{\text{Observation Model}} \; \underbrace{p(x_t|z_{1:t-1}, u_{1:t}, m)}_{\text{Motion Model}}
}$
Normalizer까지 처리하고 난 식에서, 표시된 항은 각각 Observation 모델, Motion 모델이라고 합니다. 이들은 정리 과정에서 각각 $z$(Observation)항과 $u$(Motion)항만이 남게 되기에 이런 이름이 붙었습니다. 먼저 Motion 모델부터 살펴봅시다.
1. Motion 모델 정리 - Law of Total Probability
Motion 모델만 따로 떼어 생각해 봅시다.
$\large{
p(x_t|z_{1:t-1}, u_{1:t}, m)
}$
이 항은 조건을 빼고 생각하면 사실상 어떤 조건에서의 $x_t$ 사건이 발생할 확률, 즉 $p(x_t)$입다. 이때, 재귀 형태로 만들기 위해서 새로운 항을 추가할 수 있는 Law of Total Probability 정리를 사용합니다. 이는 다음 블로그에 잘 정리되어 있습니다. 정리는 다음과 같습니다.
$\large{
P(A)=\int_{B}^{}P(A|B)P(A) \; dB
}$
이를 위의 식에 적용하여 새로운 항 $x_{t-1}$을 추가합니다.
$\large{
p(x_t|z_{1:t-1}, u_{1:t}, m)=\int_{x_{t-1}}^{}p(x_t|x_{t-1}, z_{1:t-1}, u_{1:t}, m)p(x_{t-1}| z_{1:t-1}, u_{1:t}, m) \; dx_{t-1}
}$
간단하게 표현하면 일어난 일은 다음과 같습니다.
$\large{
p(x_t)=\int_{x_{t-1}}^{}p(x_t|x_{t-1})P(x_{t-1}) \; dx_{t-1}
}$
Law of Total Probaility를 사용하여 이전 position $x_{t-1}$과의 연결고리를 만들었습니다. 이제 재귀 형태의 베이스가 갖춰졌으니, 생략 가능한 항을 찾아봅시다.
2. Motion 모델 정리 - Markov Assumption
Law of Total Probaility를 사용한 후, 도출된 식을 좀 더 줄이는데 Markov Assumption을 사용합니다. Markov Assumption은 쉽게 말하면 관계없는 항을 계속 생략하는 방법입니다. 오컴의 면도날 법칙을 정리로 만들어 놓은 듯한 이 정리를 통해 Motion 모델을 생략해 봅시다.
먼저 현재의 Motion 모델을 그래프로 나타내면 다음과 같습니다.
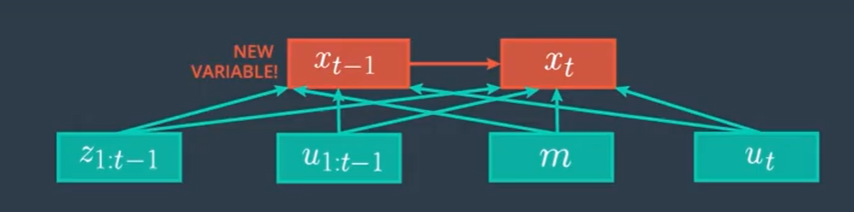
$\large{
p(x_t|z_{1:t-1}, u_{1:t}, m)=\int_{x_{t-1}}^{}p(x_t|x_{t-1}, z_{1:t-1}, u_{1:t}, m)p(x_{t-1}| z_{1:t-1}, u_{1:t}, m) \; dx_{t-1}
}$
위의 그래프에서 $z_{1:t-1}$과 $u_{1:t-1}$은 이미 $x_{t-1}$을 만드는 데 반영되어 있습니다. 따라서 이들을 $x_t$에까지 반영할 필요가 없습니다. 따라서 $z_{1:t-1}$과 $u_{1:t-1}$을 생략합니다.
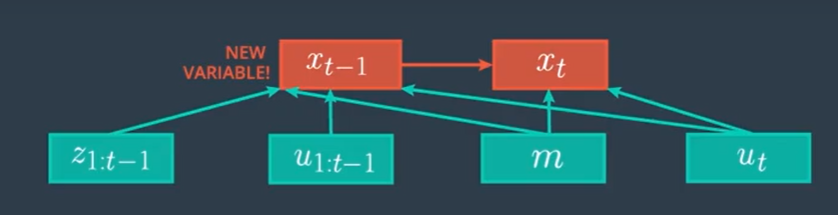
$\large{
\int_{x_{t-1}}^{}p(x_t|x_{t-1}, z_{1:t-1}, u_{1:t}, m)p(x_{t-1}| z_{1:t-1}, u_{1:t}, m) \; dx_{t-1}
}$
$\large{
\rightarrow \int_{x_{t-1}}^{}p(x_t|x_{t-1}, u_{t}, m)p(x_{t-1}| z_{1:t-1}, u_{1:t}, m) \; dx_{t-1}
}$
이제 조금 더 생략해 봅시다. 위의 그래프의 $u_t$를 봅시다. 시간 $t$에서의 Motion인 $u_t$는 $t-1$에서의 position $x_{t-1}$과 연결되어 있지만 position $x_{t-1}$의 확률함수를 구하는데는 쓸모가 없습니다. 따라서 $x_{t-1}$을 가리키는 $u_t$의 화살표를 생략할 수 있습니다.
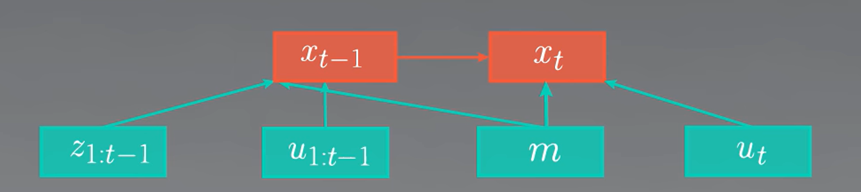
$\large{
\int_{x_{t-1}}^{}p(x_t|x_{t-1}, u_{t}, m)p(x_{t-1}| z_{1:t-1}, u_{1:t}, m) \; dx_{t-1}
}$
$\large{
\rightarrow \int_{x_{t-1}}^{}p(x_t|x_{t-1}, u_{t}, m)p(x_{t-1}| z_{1:t-1}, u_{1:t-1}, m) \; dx_{t-1}
}$
이 과정을 거치고 나면, 지금까지의 결과의 $p(x_{t-1}| z_{1:t-1}, u_{1:t-1}, m)$ 항은 익숙한 모습을 하고 있습니다. 바로 $bel(x_{t-1})$의 모습입니다. 해당 항을 $bel(x_{t-1})$으로 교체해 줍니다.
$\large{
\int_{x_{t-1}}^{}p(x_t|x_{t-1}, u_{t}, m)p(x_{t-1}| z_{1:t-1}, u_{1:t-1}, m) \; dx_{t-1}
}$
$\large{
\rightarrow \int_{x_{t-1}}^{}p(x_t|x_{t-1}, u_{t}, m) \; bel(x_{t-1}) \; dx_{t-1}
}$
이제 위에서 언급한 대로 Motion 모델에는 $z$항이 없어지고 $u$항만 남은데다, 재귀 형태의 확률함수가 되었습니다. 이전 position의 확률로부터 현재 position에 대한 확률을 도출할 수 있게 되었습니다.
시간 $t$에서의 Motion 모델
위에서 나타낸 시간 $t$에서의 Motion 모델은 이산적인 확률의 합입니다.
시간$1:t$에 따른 Motion 항은 다음과 같이 표현할 수 있습니다.
$\large{
u_{1:t}=\left \{ u_1, u_2, \cdots, u_t \right \}
}$
그리고 다시 이 항들은 이전 position에 따라서 $u_{t}^{(i)}$들로 표현될 수 있습니다.
$\large{
u_{t}=\left \{ u_{t}^{(1)}, u_{t}^{(2)}, \cdots, u_{t}^{(i)} \right \}
}$
여기서 각각의 항에 해당하는 확률은 이전 position과 현재 position 간에 오차의 *정규분포 $\times \; bel(x_{t-1})$과 같습니다. 식으로 나타내면 다음과 같습니다.
$
이전\;position과\;현재\;position\;간에\;오차의\;정규분포 = p(x_t|x_{t-1}^{(i)}, u_t, m) \;\;\;\; (Transition\;Model)
$
$\large{
u_{t}^{(i)}에\;해당하는\;이산적\;확률 = p(x_t|x_{t-1}^{(i)}, u_t, m) \; bel(x_{t-1}^{(i)})
}$
이러한 $u_{t}^{(1)} \sim u_{t}^{(i)}$에 해당하는 확률을 모두 합친 확률이 바로 위에서 정리했던 시간 $t$에서의 Motion 모델입니다.
$\large{
시간\;t에서의\;Motion\;모델=\sum_{i}^{}p(x_t|x_{t-1}^{(i)}, u_t, m) \; bel(x_{t-1}^{(i)})
}$
예시를 통해 더욱 알기 쉽게 알아보겠습니다.
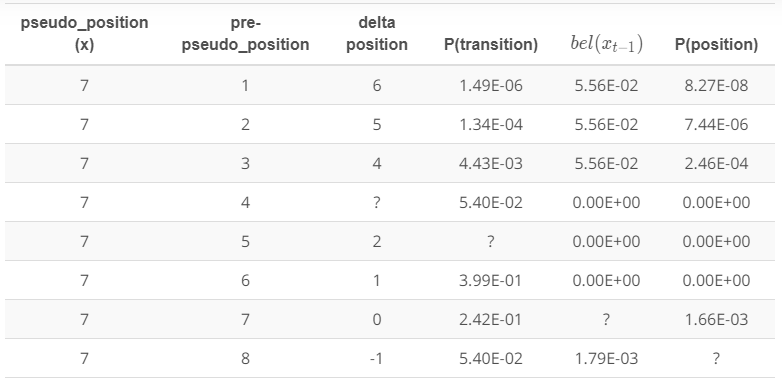
다음 표에 있는 항목들의 의미는 다음과 같습니다.
- pseudo position: position $x_t$
- pre-pseudo position: position $x_{t-1}$
- delta position: position $x_t$ - position $x_{t-1}$
- P(transition): delta position의 정규분포 결과값
- $bel(x_{t-1})$: $bel(x_{t-1})$
- P(position): P(transition)$\times\;bel(x_{t-1})$
각각의 행은 일어날 수 있는 사건을 의미합니다. 예를 들어 첫번째 행은 자동차가 position $x_{t-1}$일때 좌표 1에 있었다가, position $x_t$일때 좌표 7로 이동한 경우입니다. 나머지 항들 역시 해당 사건의 P(transition) 또는 P(position) 값입니다.
결과적으로 모든 P(position)의 합이 시간 $t$에서의 Motion 모델이 됩니다. 이 강의의 예시는 쉽게 이해시키기 위해 1차원 이동만을 봤지만, 실제로 차는 최소 2차원 이동을 하게 됩니다. 그때가 되면 더욱 어려운 계산을 해야 할 것입니다.
*정규분포: 이 강의에서는 확률밀도함수 정규분포를 사용하였습니다. 하지만 실제로는 정규분포함수를 사용할 수 없는 모델도 나옵니다. 항상 정규분포는 아니라는 점을 기억해 둡시다.
3. Observation 모델 정리 - Markov Assumption
Motion 모델의 정리를 마쳤으니 남은 항은 왼쪽의 Observation 모델입니다.
$\large{
p(x_t|z_t, z_{1:t-1}, u_{1:t}, m) = \eta \; \underbrace{p(z_t|x_t, z_{1:t-1}, u_{1:t}, m)}_{\text{Observation Model}} \; \underbrace{\int_{x_{t-1}}^{}p(x_t|x_{t-1}, u_{t}, m) \; bel(x_{t-1}) \; dx_{t-1}}_{\text{Motion Model}}
}$
이번 정리에서는 Markov Assumption만 사용합니다. 다음 그림을 봅시다.
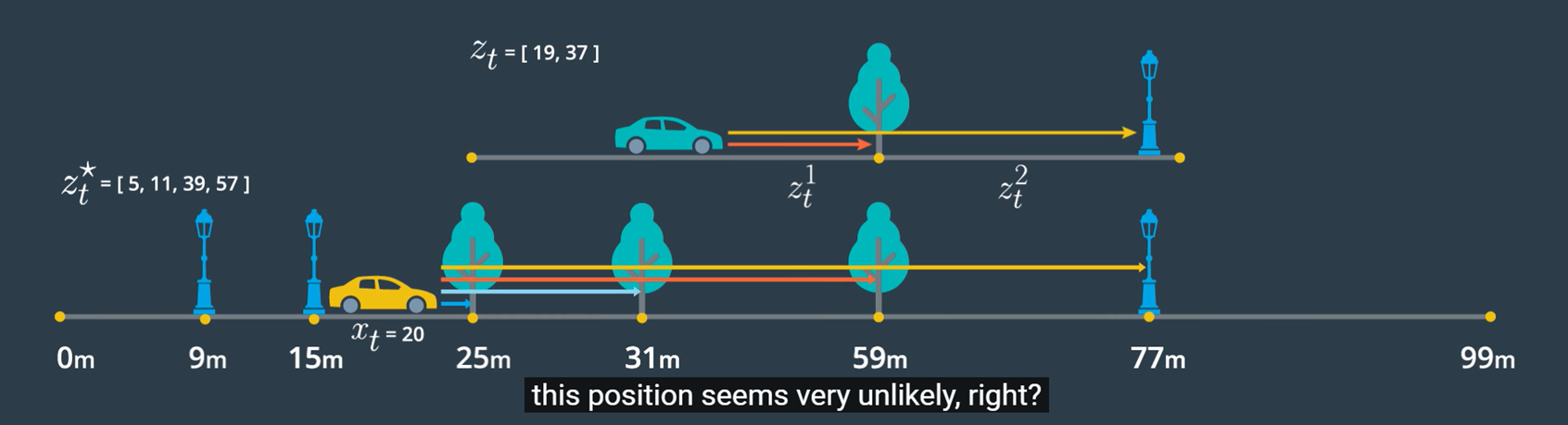
이 그림에서 $z_t$는 실제 관측값을 의미합니다. 하지만 $z_{t}^{}$는 자동차가 생각하는 관측값입니다. 자동차는 자신의 위치 $x_t$가 정확히 어디인지 모르기에 관측값을 토대로 자신의 위치를 찾아냅니다. 따라서 $x_t$는 자동차가 생각하는 자기 위치, 즉 *기대 위치라고 할 수 있습니다. 그림에서 자동차는 자신의 기대 위치 $x_t$를 20m 지점이라고 생각하고 있습니다. 이 기대 위치 $x_t$와 지도를 비교하여 landmark까지의 기대 관측값을 찾아냅니다. 이 기대 관측값 $z_{t}^{}$와 실제 관측값 $z_t$를 비교하여 관측이 맞을 확률을 도출합니다.(이부분 맞는지 모르겠음) 이를 통해서 알아낼 수 있는 점은 이 과정에서 $u_{1:t}$ 항을 전혀 사용하지 않은 것입니다. 게다가 관측은 Motion 이후에 시도하므로, $u_{1:t}$은 생략할 수 있는 항이 됩니다.
이제 Observation 모델만 따로 떼어 생각해 봅시다.
$\large{
p(z_t|x_t, z_{1:t-1}, u_{1:t}, m)
}$
우리는 위의 과정을 통해 $u_{1:t}$ 항을 생략할 수 있다는 사실을 알았습니다. 다음 그림을 참고합시다.

위의 그림의 그래프를 보면 $z_{1:t-1}$ 항은 이미 $z_t$ 항을 구성하는 데 반영되어 있습니다. 그렇다면 Markov Assumption에 의해 생략할 수 있습니다. 따라서 생략가능한 항을 생략한 Observation 모델은 다음과 같습니다.
$\large{
p(z_t|x_t, z_{1:t-1}, u_{1:t}, m)
}$
$\large{
\rightarrow p(z_t|x_t, m)
}$
아주아주 짧아졌습니다. 이제 다시 이 결과를 베이즈 정리를 적용한 $bel(x_t)$의 식에 대입해 봅시다.
Q. 자동차는 어떻게 자신의 기대 위치의 확률을 찾는 과정에서 기대 위치를 알고 있을까요?
A. 이 과정은 $p(x_t)$를 찾는 과정이지 $x_t$를 찾는 과정이 아닙니다. 따라서 $x_t$는 이미 알고 있다고 가정하고 이 과정을 수행하는 것입니다.
*기대 위치: 이 단어는 제 게시글에서만 이해를 돕기 위해 사용하는 말이고 전문적으로 사용되는 용어는 아닙니다. 다른 곳에서 사용은 자제해주시길 바랍니다…
Markov Localization의 결과
모든 정리를 끝낸 후의 결과는 다음과 같습니다.
$\large{
p(x_t|z_t, z_{1:t-1}, u_{1:t}, m) = \eta \; \underbrace{p(z_t|x_t, m)}_{\text{Observation Model}} \; \underbrace{\int_{x_{t-1}}^{}p(x_t|x_{t-1}, u_{t}, m) \; bel(x_{t-1}) \; dx_{t-1}}_{\text{Motion Model}}
}$
하지만 보통 이 공식은 알고리즘으로 많이 사용하기에, Motion 모델을 $\hat(bel)(x_{t})$로 대체하고, 앞선 과정에서 미리 계산합니다. 대체한 공식은 다음과 같습니다.
$\large{
\widehat{bel}(x_{t})=\int_{x_{t-1}}^{}p(x_t|x_{t-1}, u_{t}, m) \; bel(x_{t-1}) \; dx_{t-1}
}$
$\large{
p(x_t|z_t, z_{1:t-1}, u_{1:t}, m) = \eta \; \underbrace{p(z_t|x_t, m)}_{\text{Observation Model}} \; \underbrace{\widehat{bel}(x_{t})}_{\text{Motion Model}}
}$
알고리즘은 다음과 같습니다.

이 필터는 베이즈 정리를 사용하였기 때문에 Bayesian Filter Localization이라고도 합니다. 특징은 재귀 형태로 사전확률과 조건으로 사후확률을 구하고, 다시 구한 사후확률을 사전확률로 사용하는 방식으로 확률을 업데이트합니다. 또한 앞으로 공부할 칼만 필터, 파티클 필터 등 많은 필터의 base가 되는 필터입니다.
참고 사이트
Udacity Self-driving car nanodegree - Markov Localization(링크 공유 불가능)
준이 블로그 - [확률과 통계] 13. 전체 확률의 법칙, Law of Total Probability
[SLAM] Bayes filter(베이즈 필터)
Refstop
Deep Learning 및 SLAM을 공부하고 있습니다.













Comments