지난 게시글에 이어 EKF를 사용한 SLAM 방법을 정리하겠습니다. SLAM은 로봇의 Localization과 Map을 작성하는 것이 목적으로 실시간 결과로서 로봇의 위치가, 최종적인 결과로서 로봇이 작성한 Map을 얻을 수 있습니다. 여기서 Map은 랜드마크의 위치를 기록한 자료로서, 사람이 생각하는 시각적인 지도가 아닌 랜드마크의 위치만을 기록한 txt 파일이 될 수도 있습니다. 이러한 SLAM의 방법으로는 Kalman Filter, Particle Filter, Graph-based 3가지로 나눌 수 있습니다. 이번 게시글에서는 EKF를 사용한 SLAM을 중심으로 설명하도록 하겠습니다.

EKF for online SLAM

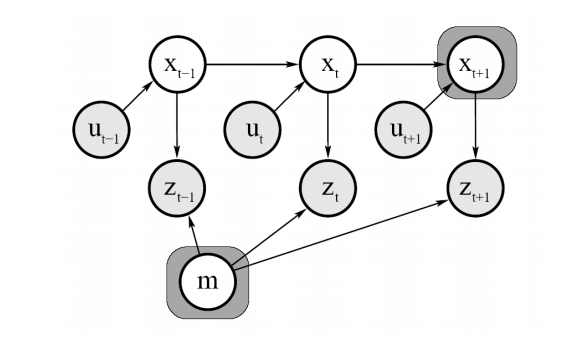
위 그림은 EKF를 이용한 online SLAM을 표현한 그림입니다. online은 실시간인 만큼 현재 로봇의 위치 state $x_t$만을 저장하는 방식으로 작동합니다. $m$은 랜드마크의 위치를 의미하고, $u_t$와 $z_t$는 각각 observation과 control input입니다. 각각 measurement model과 motion model과 관련이 있는 항입니다. 이 문제를 식으로 표현하면 다음과 같습니다.

$p(x_t, m|z_{1:t}, u_{1:t})$

즉, 처음부터 현재 시간 $t$까지의 control input과 observation을 알고 있을 때 현재 로봇의 위치 state $x_t$와 맵을 구성하는 랜드마크인 $m$을 구하는 문제입니다.

state의 표현방법

이 게시글에서 다루는 로봇의 state 모델은 2D를 기준으로 하고 있습니다. 따라서 이 로봇의 state vector는 위치와 방향을 나타내는 $x$, $y$, $\theta$로 이루어져 있는 3$\times$1 크기의 열 벡터입니다. 그리고 랜드마크의 state vector는 위치만을 나타내는 $x$, $y$로 이루어져 있는 2$\times$1 크기의 열 벡터입니다. 기본적으로, EKF SLAM에서의 state vector $x_t$는 위의 로봇 state vector, 랜드마크 state vector 두 요소로 구성되어 있습니다. 이는 위의 $p(x_t, m|z_{1:t}, u_{1:t})$ 공식에서도 볼 수 있습니다.

$\begin{align*} x_t &= (x_R, m)^T \\ &=(x,y,\theta,m_{1,x},m_{1,y},m_{2,x},m_{2,y},\cdots,m_{n,x},m_{n,y})^T \end{align*}$

따라서 랜드마크의 개수를 n이라고 할 때, state 벡터의 크기는 3+2n$\times$1이 됩니다. 이렇게 state vector가 정의되었을 때 공분산 행렬은 다음과 같이 정의됩니다.


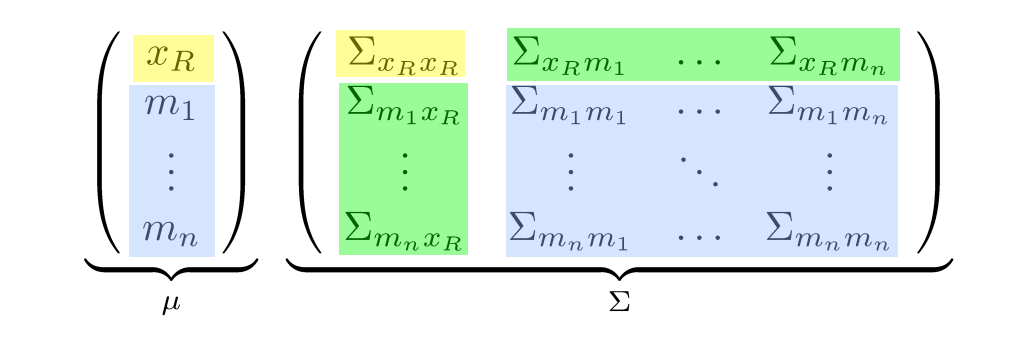
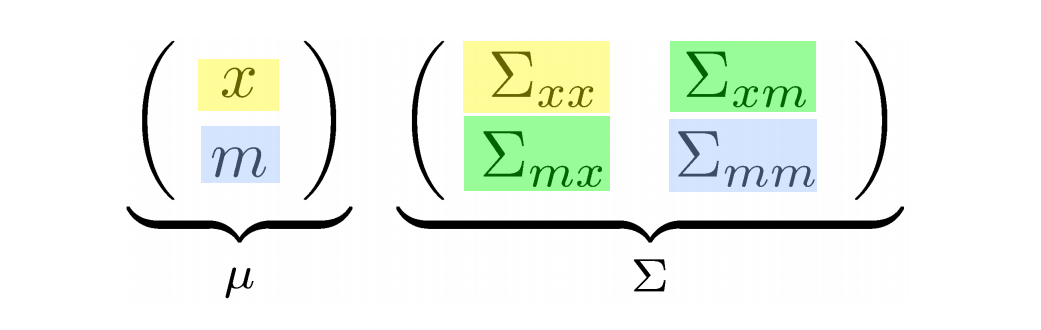
노란색으로 표시된 부분이 로봇 state에 대한 공분산, 파란색으로 표시된 부분이 랜드마크 state에 대한 공분산입니다. 지난 게시글에서 말했듯이 공분산이란 uncertainty를 나타내는 값으로 이 값이 클수록 불확실한 정보를 나타낸다고 말할 수 있습니다. 랜드마크에도 공분산이 있는 이유는 Mapping을 하는 동안 랜드마크의 위치(state) 역시 불확실한 상태이므로 계속해서 수정되어질 필요가 있기 때문입니다.

Prediction Step

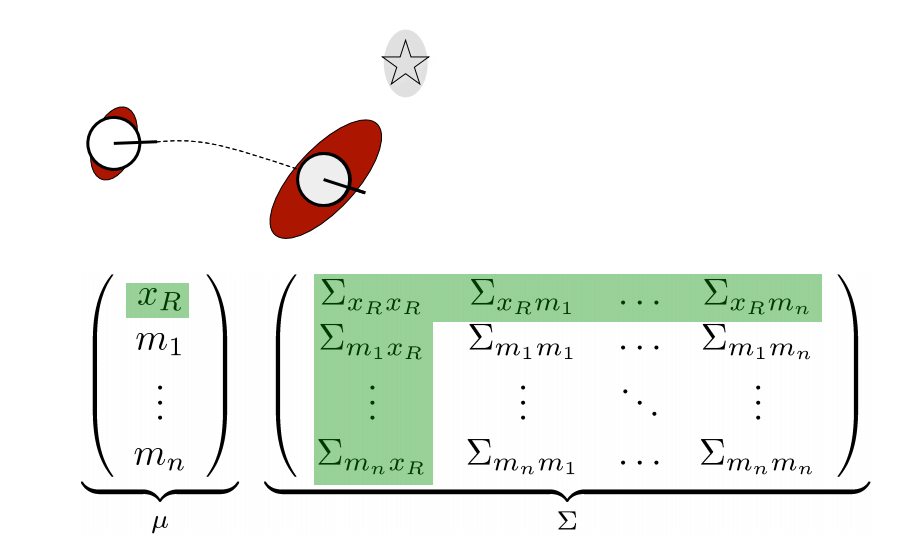
위 그림은 로봇이 이동하였을 때 prediction step 단계를 보여주고 있습니다. prediction step에서는 control input을 이용하여 예상되는 로봇의 위치를 추정하는 과정입니다. 따라서 로봇의 위치인 $x_R$과 로봇의 위치에 대한 공분산행렬 $\Sigma_{x_R x_R}$, 그리고 $x_R$이 관련되어 있는 $\Sigma_{x_R m_n}$ 공분산 행렬도 update됩니다. 아직 가장 큰 공분산 행렬인 $\Sigma_{mm}$을 건드리지 않았기 때문에 계산량이 크지 않고, 이 계산량은 랜드마크의 개수에 따라서 선형적으로 증가합니다.

Correction Step

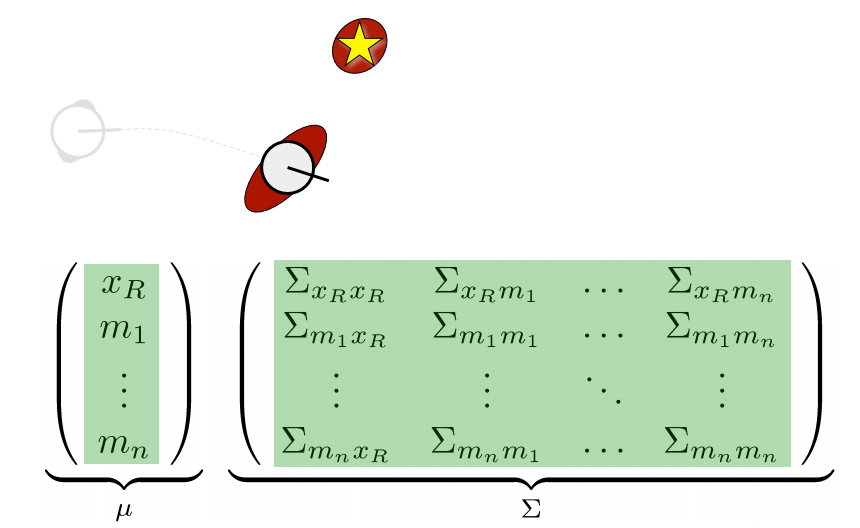
위 그림은 로봇이 랜드마크를 관측하여 얻은 데이터와 로봇이 알고 있는 랜드마크의 데이터를 비교하여 state를 보정하는 과정입니다. 이 과정에서 실제 observation의 uncertainty가 state에 반영이 되며, 랜드마크의 공분산 행렬에도 영향을 주게 됩니다. 따라서 correction단계에서는 state vector와 공분산 행렬의 모든 영역이 update됩니다. correction 단계의 계산량은 랜드마크의 숫자에 quadratic하게 증가합니다. 왜냐하면 Kalman gain을 구할 때 역행렬을 구하는 과정에서 행렬 크기에 quadratic하게 증가하기 때문입니다.

EKF SLAM Example

Example을 위한 가정

• 로봇은 2D plane 상에서 움직입니다.
• Velocity-based motion model을 사용합니다.
• 로봇은 랜드마크를 point($x$, $y$)로 인식합니다.
• Observation model은 LiDAR와 같은 Range-bearing 센서입니다.
• 관측된 랜드마크와 알고있는 map상의 랜드마크와의 대응 관계는 알고 있다고 가정합니다.
• 랜드마크의 개수는 미리 알고 있습니다.

초기화

SLAM의 가정에서 랜드마크의 개수는 미리 알고 있다고 하였으므로, state vector와 공분산행렬을 고정된 크기로 취급할 수 있습니다. state vector의 크기는 3+2n$\times$1, 공분산행렬의 크기는 3+2n$\times$3+2n입니다. 또한 로봇의 시작 위치는 원점이 되므로 state vector를 3+2n$\times$1 크기의 영행렬로 초기화합니다.

$\mu_0=(0,0,0,0,\cdots,0)^T$

공분산행렬의 경우 로봇의 state를 (0,0,0)으로 확실히 알고 있고(uncertainty 매우 작음), 랜드마크는 아예 어디 있는지 모른다(uncertainty 매우 큼)고 가정하여, $\Sigma_{x_R x_R}$을 3$\times$3 크기의 영행렬로, $\Sigma_{mm}$을 2n$\times$2n 크기의 무한대 대각행렬로 초기화합니다.

$\Sigma_0=\begin{pmatrix} 0 & 0 & 0 & 0 & 0 & \cdots & 0\\ 0 & 0 & 0 & 0 & 0 & \cdots & 0\\ 0 & 0 & 0 & 0 & 0 & \cdots & 0\\ 0 & 0 & 0 & \infty & 0 & \cdots & 0\\ 0 & 0 & 0 & 0 & \infty & \cdots & 0\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\ 0 & 0 & 0 & 0 & 0 & \cdots & \infty \end{pmatrix}$

Extended Kalman Filter (EKF) 과정

$\begin{align*} 1&: Extended Kalman filter(\mu_{t-1}, \Sigma_{t-1}, u_t, z_t) \\ & [Prediction\;step] \\ 2&: \overline{\mu}_t=g(u_t, \mu_{t-1}) \\ 3&: \overline{\Sigma}_t=G_t\Sigma_{t-1}G_t^T+R_t \\ & [Correction\;step] \\ 4&: K_t=\overline{\Sigma}_tH_t^T(H_t\overline{\Sigma}_tH_t^T+Q_t)^{-1}\\ 5&: \mu_t = \overline{\mu}_t+K_t(z_t-h(\overline{\mu}_t)) \\ 6&: \Sigma_t = (I-K_tH_t)\overline{\Sigma}_t \\ 7&: return\;\mu_t, \Sigma_t \end{align*}$

이전 게시글에서 설명했었던 EKF 알고리즘에 따르면, 입력 $\mu_t{t-1}, \Sigma_{t-1}, u_t, z_t$ 중에서 $\mu_t{t-1}, \Sigma_{t-1}$을 구했고, $u_t, z_t$에 대한 입력은 각각 motion model, observation model에 관한 항이므로, 센서 입력($u_t$: 엔코더, $z_t$: 카메라, LiDAR)에 의해 결정되므로, prediction 단계와 correction 단계를 설명할 때 더욱 자세히 설명하겠습니다.

State(Mean) Prediction

로봇의 motion model을 나타낼 때는 주로 다음 2가지를 사용합니다.

• Odometry-based model
• Velocity-based model
  Odometry-based model은 로봇 또는 자동차의 바퀴에 달린 wheel encoder 센서 데이터를 이용한 모델이며, Velocity-based model은 imu와 같은 관성 센서(선속도, 각속도를 측정해줌)를 이용한 모델입니다. Velocity-based model은 wheel encoder와 같은 Odometry-based model을 사용할 수 없을 때 주로 사용하며, Odometry-based model보다 Velocity-based model이 더 정확한 편입니다.
  이번 예시에서 사용한 모델은 Velocity-based model입니다. Velocity-based model은 다음과 같습니다.

$\begin{bmatrix} x_t\\ y_t\\ \theta_t \end{bmatrix}=\begin{bmatrix} x_{t-1}\\ y_{t-1}\\ \theta_{t-1} \end{bmatrix}+\begin{bmatrix} -\frac{v_t}{w_t}sin \theta_{t-1}+\frac{v_t}{w_t}sin(\theta_{t-1}+w_t \Delta t)\\ -\frac{v_t}{w_t}cos \theta_{t-1}-\frac{v_t}{w_t}cos(\theta_{t-1}+w_t \Delta t)\\ w_t \Delta t \end{bmatrix}$

위의 motion model은 로봇의 위치에 대한 정보만을 갖고 있는 3$\times$1 크기의 vector입니다. 이 vector를 3+2n$times$1 크기의 state vector $x_t$에 더하기 위해서는 동차 행렬 $F_x$ 행렬을 이용합니다.

$F_x = \begin{bmatrix} 1 & 0 & 0 & 0 & \cdots & 0\\ 0 & 1 & 0 & 0 & \cdots & 0\\ 0 & 0 & 1 & 0 & \cdots & 0 \end{bmatrix}^T$ $\begin{bmatrix} x_t\\ y_t\\ \theta_t \end{bmatrix}=\begin{bmatrix} x_{t-1}\\ y_{t-1}\\ \theta_{t-1} \end{bmatrix}+F_x\begin{bmatrix} -\frac{v_t}{w_t}sin \theta_{t-1}+\frac{v_t}{w_t}sin(\theta_{t-1}+w_t \Delta t)\\ -\frac{v_t}{w_t}cos \theta_{t-1}-\frac{v_t}{w_t}cos(\theta_{t-1}+w_t \Delta t)\\ w_t \Delta t \end{bmatrix}$

위와 같이 $F_x$ 행렬을 이용함으로서 control input에 의한 로봇 위치의 state만 변경되었습니다.

공분산 행렬 prediction

3번 단계에서 공분산을 구하기 위해선, motion model의 자코비안 행렬인 $G_t$와 process noise인 $R_t$가 필요합니다. 이때 사용한 motion model은 Velocity-based motion model이므로, 이 motion model의 자코비안 행렬은 다음과 같습니다.

$G_t^x=\frac{\partial g(u_t,\mu_{t-1})}{\partial x_{t-1}}=\begin{pmatrix} 1 & 0 & -\frac{v_t}{w_t}cos \theta_{t-1}+\frac{v_t}{w_t}cos(\theta_{t-1}+w_t \Delta t)\\ 0 & 1 & -\frac{v_t}{w_t}sin \theta_{t-1}+\frac{v_t}{w_t}sin(\theta_{t-1}+w_t \Delta t)\\ 0 & 0 & 1 \end{pmatrix}$

하지만 이때 구한 $G_t^x$는 3$\times$3 행렬이므로, 3+2n$\times$3+2n 크기에 맞춰 주기 위해 다음과 같이 행렬을 수정합니다.

$G_t=\begin{pmatrix} G_t^x & 0\\ 0 & I\\ \end{pmatrix}$

또한 process noise $R_t$은 다음과 같이 정의됩니다.

$R_t=V_tM_tV_t^T$

여기서 $V_t$는 $g(u_t,\mu_{t-1})$을 $u_t$로 편미분한 값입니다. Velocity-based model에서 $u_t$는 $(v_t, w_t)$로 이루어져 있으므로, 미분한 값은 다음과 같습니다.

$V_t=\frac{\partial g(u_t,\mu_{t-1})}{\partial u_t}=\begin{pmatrix} \frac{-sin\theta_{t-1}+sin(\theta_{t-1}+w_t\Delta t)}{w_t} & \frac{v_t(sin\theta_{t-1}-sin(\theta_{t-1}+w_t\Delta t))}{w_t^2}+\frac{v_t\Delta tcos(\theta_{t-1}+w_t\Delta t)}{w_t}\\ \frac{cos\theta_{t-1}-cos(\theta_{t-1}+w_t\Delta t)}{w_t} & \frac{v_t(-cos\theta_{t-1}+cos(\theta_{t-1}+w_t\Delta t))}{w_t^2}+\frac{v_t\Delta tsin(\theta_{t-1}+w_t\Delta t)}{w_t}\\ 0 & 1 \end{pmatrix}$

결국 $R_t$의 크기 역시 3$\times$3이므로, 동차 행렬 $F_x$을 곱하여 크기를 수정하여 3번 단계의 연산을 수행합니다.

$\overline{\Sigma}_t=G_t\Sigma_{t-1}G_t^T+F_xR_tF_x^T$

State(Mean) Correction

EKF SLAM의 correction 단계의 과정은 다음과 같습니다.

1. $c_t^i=j$는 $t$시점에서 $i$번째로 측정된 랜드마크이며 전체 랜드마크에서 $j$번째 index를 갖습니다.
2. 만약 랜드마크가 이전에 관측되지 않았던 랜드마크이면 현재 로봇의 위치를 기반으로 초기화합니다. 즉 랜드마크 initialization입니다.
3. 예상되는 observation을 계산합니다.
4. 비선형 함수 $h(x_t)$의 자코비안 행렬을 계산합니다.
5. Kalman gain을 계산하고 correction process를 진행합니다. 이 예제에서는 LiDAR 센서와 같은 Range-bearing observation 센서를 기반으로 합니다. Range-bearing observation model은 다음과 같습니다.

$z_t^i=\begin{pmatrix} r_t^i\\ \phi_t^i \end{pmatrix}$

$r_t^i$는 로봇으로부터 랜드마크의 거리, $\phi_t^i$는 로봇의 헤딩 각도로부터 랜드마크까지의 방향을 의미합니다. 센서로부터 랜드마크의 데이터가 획득되었으나 이전에 관측되지 않았던 랜드마크라면 아래 식을 통해 랜드마크의 global 위치를 계산하여 state에 등록합니다.

$\begin{pmatrix} \overline{\mu}_{j,x}\\ \overline{\mu}_{j,y} \end{pmatrix}=\begin{pmatrix} \overline{\mu}_{t,x}\\ \overline{\mu}_{t,y} \end{pmatrix}+\begin{pmatrix} r_t^icos(\phi_t^i+\overline{\mu}_{t,\theta})\\ r_t^isin(\phi_t^i+\overline{\mu}_{t,\theta}) \end{pmatrix}$

$\overline{\mu}j$는 $j$번째 랜드마크의 위치이고 위 state vector에서 $m_j$항으로 나타낼 수 있습니다. $\overline{\mu}{t,x}$, $\overline{\mu}{t,y}$, $\overline{\mu}{t,\theta}$는 각각 현재 시점에서 로봇의 $x$, $y$, $\theta$(heading)를 의미합니다. Range-bearing observation model은 다음과 같이 계산합니다.

$\delta=\begin{pmatrix} \delta_x \\ \delta_y \end{pmatrix}=\begin{pmatrix} \overline{\mu}_{j,x} - \overline{\mu}_{t,x} \\ \overline{\mu}_{j,y} - \overline{\mu}_{t,y} \end{pmatrix}$ $q=\delta^T\delta$ $\hat{z}_t^i=\begin{pmatrix} \sqrt{q}\\ arctan(\frac{\delta_y}{\delta_x}-\overline{\mu}_{t,\theta} \end{pmatrix}=h(\overline{\mu}_t)$

$\delta$는 로봇의 위치와 랜드마크의 위치 차를 의미하며, $\sqrt{q}$는 로봇과 랜드마크의 거리를 의미합니다. 따라서 $h(\overline{\mu}t)$는 비선형 observation 모델이며, 현재 로봇의 위치와 랜드마크의 거리를 알고 있을 때 이 observation 모델을 이용하여 예상되는 센서의 observation을 계산할 수 있습니다. 여기서 $\overline{\mu}_t$는 로봇의 현재 위치정보($\overline{\mu}{t,x}$, $\overline{\mu}{t,y}$, $\overline{\mu}{t,\theta}$)와 랜드마크의 위치 ($\overline{\mu}{j,x}$, $\overline{\mu}{j,y}$)를 포함하고 있는 5$\times$1크기의 vector입니다.

이 observation model의 선형화 과정을 통해 $h(\overline{\mu}_t)$의 자코비안 행렬을 구하면 다음과 같습니다.

$^{low}\textrm{H}_t^i=\frac{\partial h(\overline{\mu}_t)}{\partial \overline{\mu}_t}=\begin{pmatrix} \frac{\partial \sqrt{q}}{\partial \overline{\mu}_{t,x}} & \frac{\partial \sqrt{q}}{\partial \overline{\mu}_{t,y}} & \frac{\partial \sqrt{q}}{\partial \overline{\mu}_{t,\theta}} & \frac{\partial \sqrt{q}}{\partial \overline{\mu}_{j,x}} & \frac{\partial \sqrt{q}}{\partial \overline{\mu}_{j,y}} \\ \frac{\partial arctan(\frac{\delta_y}{\delta_x}-\overline{\mu}_{t,\theta})}{\partial \overline{\mu}_{t,x}} & \frac{\partial arctan(\frac{\delta_y}{\delta_x}-\overline{\mu}_{t,\theta})}{\partial \overline{\mu}_{t,y}} & \frac{\partial arctan(\frac{\delta_y}{\delta_x}-\overline{\mu}_{t,\theta})}{\partial \overline{\mu}_{t,\theta}} & \frac{\partial arctan(\frac{\delta_y}{\delta_x}-\overline{\mu}_{t,\theta})}{\partial \overline{\mu}_{j,x}} & \frac{\partial arctan(\frac{\delta_y}{\delta_x}-\overline{\mu}_{t,\theta})}{\partial \overline{\mu}_{j,y}} \end{pmatrix}=\frac{1}{q}\begin{pmatrix} -\sqrt{q}\delta_x & -\sqrt{q}\delta_y & 0 & \sqrt{q}\delta_x & \sqrt{q}\delta_y \\ \delta_y & \delta_x & -q & -\delta_y & \delta_x \end{pmatrix}$

$^{low}\textrm{H}t^i$에서 low는 아직 크기를 조정하기 전의 행렬이라는 의미로 사용되었습니다. 자코비안 행렬 $^{low}\textrm{H}_t^i$의 크기는 2$\times$5이므로 EKF correction의 update과정에 적용시키기 위해서 $F{x,j}$ 행렬을 이용하여 행렬의 크기를 조절합니다.

$H_t^i=^{low}\textrm{H}_t^iF_{x,j}$ $F_{x,j}=\begin{pmatrix} 1 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0\\ 0 & 1 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0\\ 0 & 0 & 1 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0\\ 0 & 0 & 0 & 0 & \cdots & 0 & 1 & 0 & 0 & \cdots & 0\\ 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 1 & 0 & \cdots & 0 \end{pmatrix}$

$F_{x,j}$ 행렬에서 1~3행은 로봇의 위치에 대한 자코비안 term을, 4~5 행은 랜드마크에 대한 자코비안 term을 원하는 위치에 입력하기 위함이여, 랜드마크의 index가 $j$인 경우 4~5행의 2$\times$2 단위행렬은 3+2(j-1)열 다음에 위치하게 됩니다. $F_{x,j}$ 행렬이 곱해진 $H_t^i$의 크기는 2$\times$3+2n입니다. 이 크기가 조절된 $H_t^i$행렬을 이용하여 칼만 게인을 구하고(4번 과정) EKF의 5, 6번 과정을 통해 최종 state와 공분산 행렬을 계산할 수 있습니다.

참고 사이트

Jinyoung - [SLAM] Motion & Observation model Jinyoung - [SLAM] Extended Kalman Filter(EKF) SLAM

Refstop

Deep Learning 및 SLAM을 공부하고 있습니다.

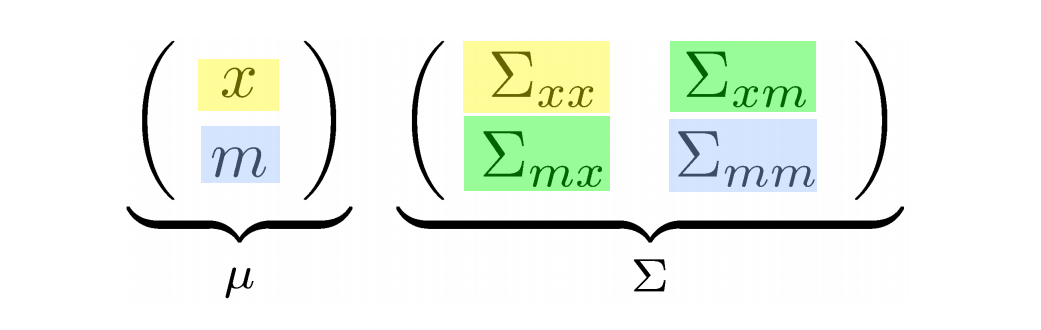
Comments

  Write a comment ...