지난 게시글에 이어 CNN의 구성과 LeNet-5를 예시로 파라미터를 계산해 보겠습니다.
input 1 is the X coordinate of the point,
Input 2 is the y coordinate of the point,
^^^왜인지 버그가 나서 아무말이나 지껴둔것
1. CNN의 구성
CNN의 구성을 공부하는 예시로서 대표적으로 사용되는 LeNet-5 모델으로 정리하겠습니다.
LeNet-5 네트워크란?
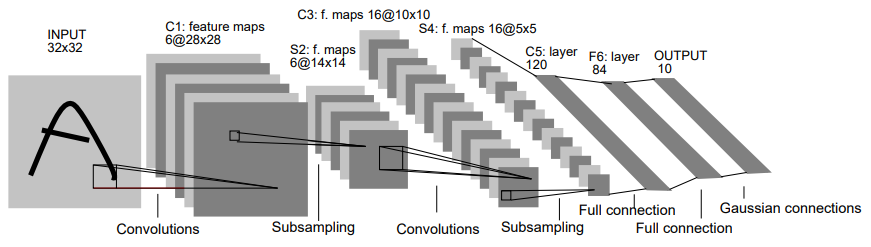
LeNet-5 네트워크는 CNN을 처음으로 개발한 Yann Lecun 연구팀이 개발한 CNN 알고리즘의 이름입니다. 이 알고리즘이 소개된 논문 제목은 Gradient-based learning applied to document recognition”입니다.
LeNet-5 네트워크는 Input-C1-S2-C3-S4-C5-F6-Output으로 이루어져 있고, Convolution layer, Pooling layer 두 쌍(C1-S2-C3-S4)과 Flatten layer(C5), Fully Connected layer(F6) 1개로 구성되어 있습니다. 원래 논문에서는 활성화 함수로서 tanh 함수를 사용했지만, 제 코드에서는 ReLU 함수를 사용하였습니다.
from keras.models import Sequential
from keras.layers.convolutional import Conv2D
from keras.layers.convolutional import MaxPooling2D
from keras.layers import Dense
from keras.layers import Flatten
model = keras.Sequential()
model.add(layers.Conv2D(filters=6, kernel_size=(3, 3), activation='relu', input_shape=(64,64,3)))
model.add(layers.MaxPooling2D(pool_size=(2, 2)))
model.add(layers.Conv2D(filters=16, kernel_size=(3, 3), activation='relu'))
model.add(layers.MaxPooling2D(pool_size=(2, 2)))
model.add(layers.Flatten())
model.add(layers.Dense(units=120, activation='relu'))
model.add(layers.Dense(units=84, activation='relu'))
model.add(layers.Dense(units=10, activation = 'softmax'))
실제 사용결과는 나중에 올리도록 하겠습니다….
2. CNN 입출력, 파라미터 계산
사용한 예시에서의 입출력 표를 정리하면 다음과 같습니다.
| layer |
Input Channel |
Filter |
Output Channel |
Stride |
Max Pooling |
Activation Function |
| Convolution Layer 1 |
3 |
(3,3) |
6 |
1 |
X |
relu |
| Max Pooling Layer 1 |
6 |
X |
6 |
1 |
(2,2) |
X |
| Convolution Layer 2 |
6 |
(4,4) |
16 |
1 |
X |
relu |
| Max Pooling Layer 2 |
16 |
X |
16 |
1 |
(2,2) |
X |
| Flatten |
X |
X |
X |
X |
X |
X |
| Fully Connected layer |
X |
X |
X |
X |
X |
softmax |
Convolution layer의 학습 파라미터 수는 입력채널수 $\times$ 필터 폭 $\times$ 필터 높이 $\times$ 출력채널수로 계산됩니다.
2.1 Layer 1의 Shape와 파라미터
Layer 1은 1개의 Convolution layer와 1개의 Pooling layer로 구성되어 있습니다.
2.1.1 Convolution layer 1
Convolution layer 1의 기본 정보는 다음과 같습니다.
- 입력 데이터 Shape = (64,64,3)
- 입력 채널 = 3
- 필터 = (3,3)
- 출력 채널 = 6
- Stride = 1
입력 이미지에 Shape가 (3,3)인 필터를 6개 적용할 경우에, 출력 데이터(Activation Map)의 Shape를 계산하는 과정은 다음과 같습니다.
$Row\;Size=\frac{N-F}{Stride}+1=\frac{64-3}{1}+1=62$
$Column\;Size=\frac{N-F}{Stride}+1=\frac{64-3}{1}+1=62$
위 식으로 계산된 Activation Map 사이즈는 (62,62,6)입니다. 따라서 이 레이어의 학습 파라미터는 다음과 같이 계산할 수 있습니다.
- 입력 채널: 3
- 출력 데이터(Activation Map) Shape: (62,62,6)
- 학습 파라미터: 162개 (3$\times$3$\times$3$\times$6)
2.1.2 Max Pooling layer 1
Max Pooling layer 1의 입력 데이터 Shape은 (62,62,6)입니다. 채널 수는 바뀌지 않고, Max Pooling 사이즈가 (2,2)이기 때문에 출력 데이터 크기는 다음과 같습니다.
$Row\;Size=\frac{62}{2}=31$
$Column\;Size=\frac{62}{2}=31$
위 식으로 계산된 출력 사이즈는 (31,31,6)입니다. 따라서 이 레이어의 학습 파라미터는 다음과 같이 계산할 수 있습니다.
- 입력 채널: 6
- 출력 데이터 Shape: (31,31,6)
- 학습 파라미터: 0개
2.2 Layer 2의 Shape와 파라미터
Layer 2도 마찬가지로 Convolution layer와 Pooling layer로 구성되어 있습니다.
2.2.1 Convolution layer 2
Convolution layer 2의 기본 정보는 다음과 같습니다.
- 입력 데이터 Shape = (31,31,6)
- 입력 채널 = 6
- 필터 = (4,4)
- 출력 채널 = 16
- Stride = 1
입력 이미지에 Shape가 (4,4)인 필터를 16개 적용할 경우에, 출력 데이터(Activation Map)의 Shape를 계산하는 과정은 다음과 같습니다.
$Row\;Size=\frac{N-F}{Stride}+1=\frac{31-4}{1}+1=28$
$Column\;Size=\frac{N-F}{Stride}+1=\frac{31-4}{1}+1=28$
위 식으로 계산된 Activation Map 사이즈는 (28,28,16)입니다. 따라서 이 레이어의 학습 파라미터는 다음과 같이 계산할 수 있습니다.
- 입력 채널: 6
- 출력 데이터(Activation Map) Shape: (28,28,16)
- 학습 파라미터: 1536개 (6$\times$4$\times$4$\times$16)
2.2.2 Max Pooling layer 2
Max Pooling layer 1의 입력 데이터 Shape은 (28,28,16)입니다. 채널 수는 바뀌지 않고, Max Pooling 사이즈가 (2,2)이기 때문에 출력 데이터 크기는 다음과 같습니다.
$Row\;Size=\frac{28}{2}=14$
$Column\;Size=\frac{28}{2}=14$
위 식으로 계산된 출력 사이즈는 (14,14,16)입니다. 따라서 이 레이어의 학습 파라미터는 다음과 같이 계산할 수 있습니다.
- 입력 채널: 16
- 출력 데이터 Shape: (14,14,16)
- 학습 파라미터: 0개
2.3 Flatten layer
Flatten layer는 CNN의 데이터를 Fully Connected Nerual Network에 사용되는 1차원 벡터로 바꿔주는 layer입니다. 파라미터는 존재하지 않고 이전 layer의 출력을 1차원 벡터로 바꾸는 역할만 합니다.
- 입력 데이터 Shape: (14,14,16)
- 출력 데이터 Shape: (3136,1)
원래 LeNet-5 네트워크에서는 Flatten 층의 입력 데이터 Shape와 같은 크기의 필터를 Convolution하고 출력 채널을 조절하여 1차원 벡터의 형태로 변환합니다. 하지만 Flatten 함수로도 충분히 이미지의 특성을 지닌 1차원 벡터로 변환할 수 있으므로 Flatten 함수를 사용합니다.
2.4 Fully Connected layer(Softmax layer)
마지막 출력층에 해당하는 FNN입니다. 입력 데이터의 class를 분류해야 하는 layer이기 때문에 Softmax 함수를 사용하여 출력층을 구성합니다. 입력 데이터의 Shape는 이전 Flatten layer의 출력인 (3136,1)입니다. 최종 출력 데이터는 원래 입력 데이터의 분류 class만큼이 되므로, 예를 들어 분류할 class가 10개라면 출력 데이터의 Shape는 (10,1)이 됩니다. 파라미터를 계산하면 다음과 같습니다.
- 입력 데이터 Shape: (3136,1)
- 출력 데이터 Shape: (10,1)
- Softmax layer의 파라미터 수: 31360개 (3136$\times$10)
| layer |
Input Channel |
Filter |
Output Channel |
Stride |
Max Pooling |
Activation Function |
Input Shape |
Output Shape |
파라미터 수 |
| Conv1 |
3 |
(3,3) |
6 |
1 |
X |
relu |
(64,64,3) |
(62,62,6) |
162 |
| MaxPooling1 |
6 |
X |
6 |
1 |
(2,2) |
X |
(62,62,6) |
(31,31,6) |
0 |
| Conv2 |
6 |
(4,4) |
16 |
1 |
X |
relu |
(31,31,6) |
(28,28,16) |
1536 |
| MaxPooling2 |
16 |
X |
16 |
1 |
(2,2) |
X |
(28,28,16) |
(14,14,16) |
0 |
| Flatten |
X |
X |
X |
X |
X |
X |
(14,14,16) |
(3136,1) |
0 |
| FC |
X |
X |
X |
X |
X |
softmax |
(3136,1) |
(10,1) |
31360 |
| 합계 |
X |
X |
X |
X |
X |
X |
X |
X |
33058 |
4. Fully Connected Nerual Network와의 비교
이 모델을 FNN의 파라미터 수와 비교한다면, 우선 입력층의 데이터가 (64,64,3)이므로 $64^2\times3=12288$개의 원소를 가진 1차원 벡터가 됩니다. 또한 이 벡터를 Fully Connected layer에 입력하여 class 개수가 10개인 출력을 갖는다면 파라미터 수는 $12288\times10=122880$개가 됩니다. layer를 하나만 가지고 있음에도 불구하고 CNN 구조의 네트워크보다 약 4배 더 많은 연산량을 가지게 됩니다. 따라서 이러한 점에서 CNN은 FNN에 비해 학습이 쉽고 네트워크 처리 속도가 빠르다는 장점을 갖고 있습니다.
참고 사이트
TAEWAN.KIM 블로그 - “CNN, Convolutional Neural Network 요약”
Refstop
Deep Learning 및 SLAM을 공부하고 있습니다.



Comments