Deep Nerual Network
지금까지 정리한 Nerual Network는 모두 layer가 하나뿐인 단층 신경망(Single-Layer Perceptron)입니다. 하지만 단층 신경망으로는 비선형 모델을 구현할 수 없습니다. 지난 게시글에서 언급한 바와 같이 비선형 모델은 입력층(Input layer), 은닉층(Hidden layer), 출력층(Output layer)으로 이루어진 $^{1)}$심층 신경망(Deep Neural Network)으로 구현할 수 있습니다. 따라서 인공 신경망의 성능 향상을 위해서는 심층 신경망의 사용은 필수적이라고 할 수 있습니다.
ReLU Activation Function
심층 신경망에 대해서 정리하기 전에 ReLU 활성화 함수에 대해서 알아보고 넘어가겠습니다. 활성화 함수는 각 층의 신경망의 출력을 결정하는 함수입니다. 또한 활성화 함수가 없다면 심층 신경망은 $y=W_{1}W_{2}W_{3} \cdots x=Wx$가 되므로 비선형 모델이라고 볼 수 없는 결과가 나옵니다. 이러한 문제를 해결하기 위해서 넣은 활성화 함수이지만, 지금까지 우리가 잘 사용했던 Sigmoid 활성화 함수에는 단점이 있습니다. 다음은 Sigmoid 함수의 미분 그래프를 나타낸 것입니다.
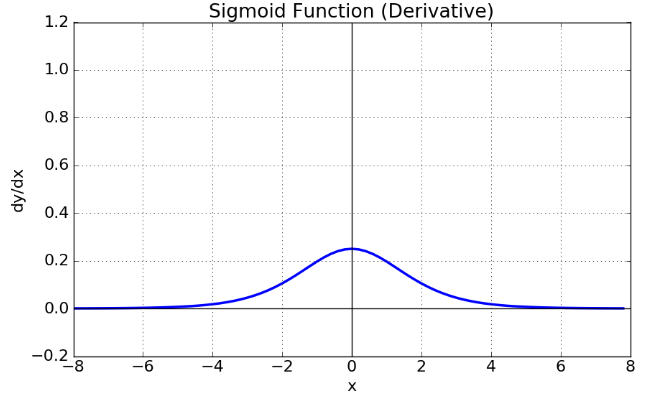
Sigmoid 함수의 단점은 미분값의 범위가 0~0.25라는 점입니다. Cross-Entropy 오차 역전파 방법을 사용할 때, 활성화 함수의 미분값을 곱해주게 됩니다. 이때 활성화 함수의 미분값이 항상 1보다 작은 경우, 바로 Sigmoid 함수같은 경우 심층 신경망의 layer가 많을수록 오차에 대한 가중치의 미분, 즉 가중치가 오차에 영향을 미치는 성분이 점점 작아지고, layer가 너무 많은 경우 오차의 미분값이 0에 수렴하게 됩니다. 이 현상이 바로 기울기 소실(Gradient Vanishing)입니다.
이러한 점을 해결하기 위해서 사용하는 활성화 함수가 바로 ReLU(Rectified Linear Unit) 함수입니다. ReLU함수의 그래프는 다음과 같은 형태입니다.
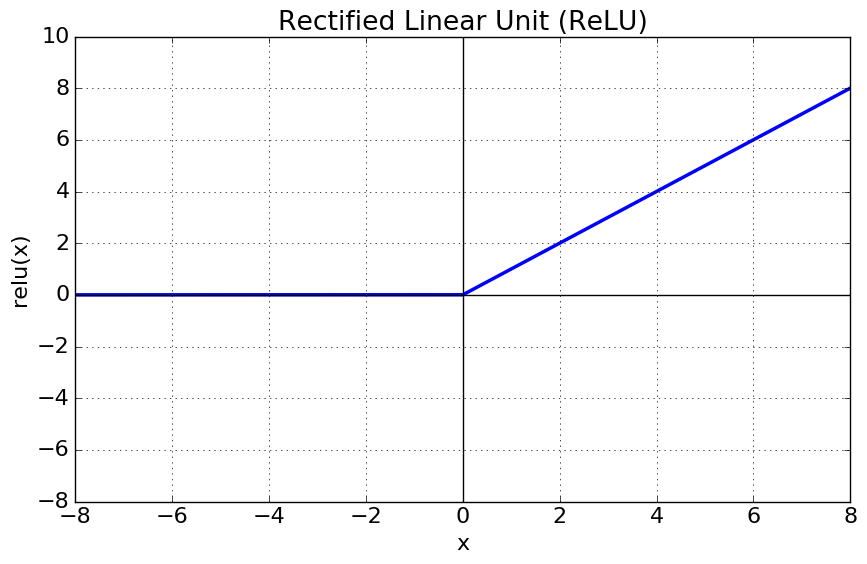
기울기 소실의 근본적인 문제점은 Sigmoid 함수의 미분값 범위 0~0.25 때문에 발생했습니다. 하지만 ReLU 함수는 활성화되었을 때 값이 1, 비활성화 되었을 때 값이 0이므로 기울기 소실 문제를 해결할 수 있습니다. 역전파 연산의 결과값, 즉 가중치에 대한 오차의 미분값이 작아지지 않기 때문에 layer 개수에 관계없이 역전파 연산의 결과를 얻을 수 있습니다. 실제로 가장 많이 사용하는 활성화 함수 역시 ReLU 함수입니다.
다시 심층 신경망의 본론으로….
방금 알아본 바와 같이 ReLU 활성화 함수를 사용하여 심층 신경망을 구성합니다. 구성된 신경망의 형태는 이전 게시글의 비선형 모델 - 다층 신경망의 그림과 별 다를 바가 없지만, 아무래도 괴발개발 그린 그림(…)보다는 구글에서 퍼온 그림이 눈이 편할 것 같아 준비했습니다.
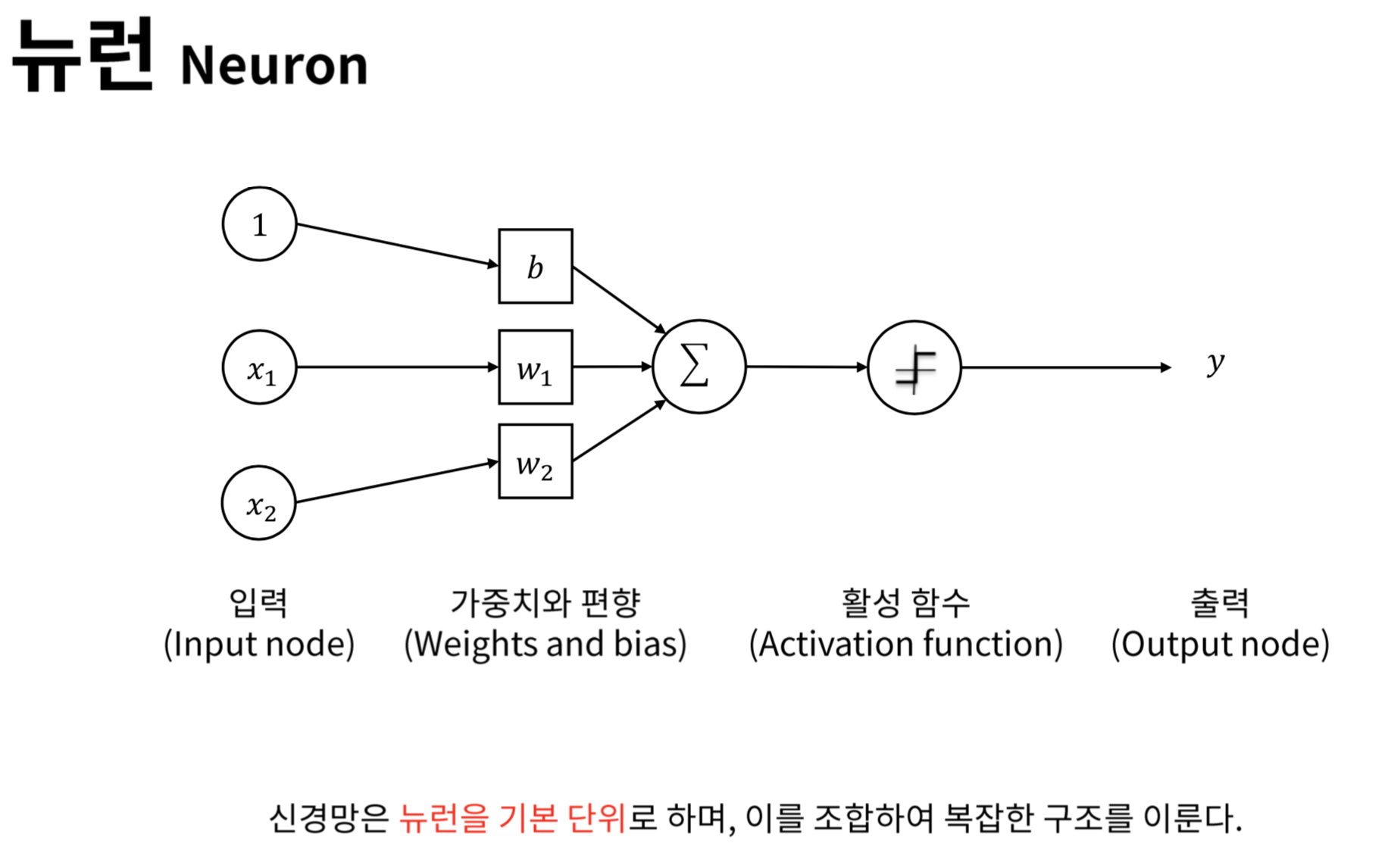
먼저 각각의 뉴런의 구성을 그린 이미지를 준비했습니다. 위의 이미지가 바로 layer가 하나뿐인 신경망, 단층 신경망입니다. 이전 게시글에 정리했던 내용이지만, 저도 오랜만에 작성하다 보니 복습할 이미지가 필요했습니다. 이러한 뉴런을 이어붙여 만든 신경망은 다음과 같습니다.
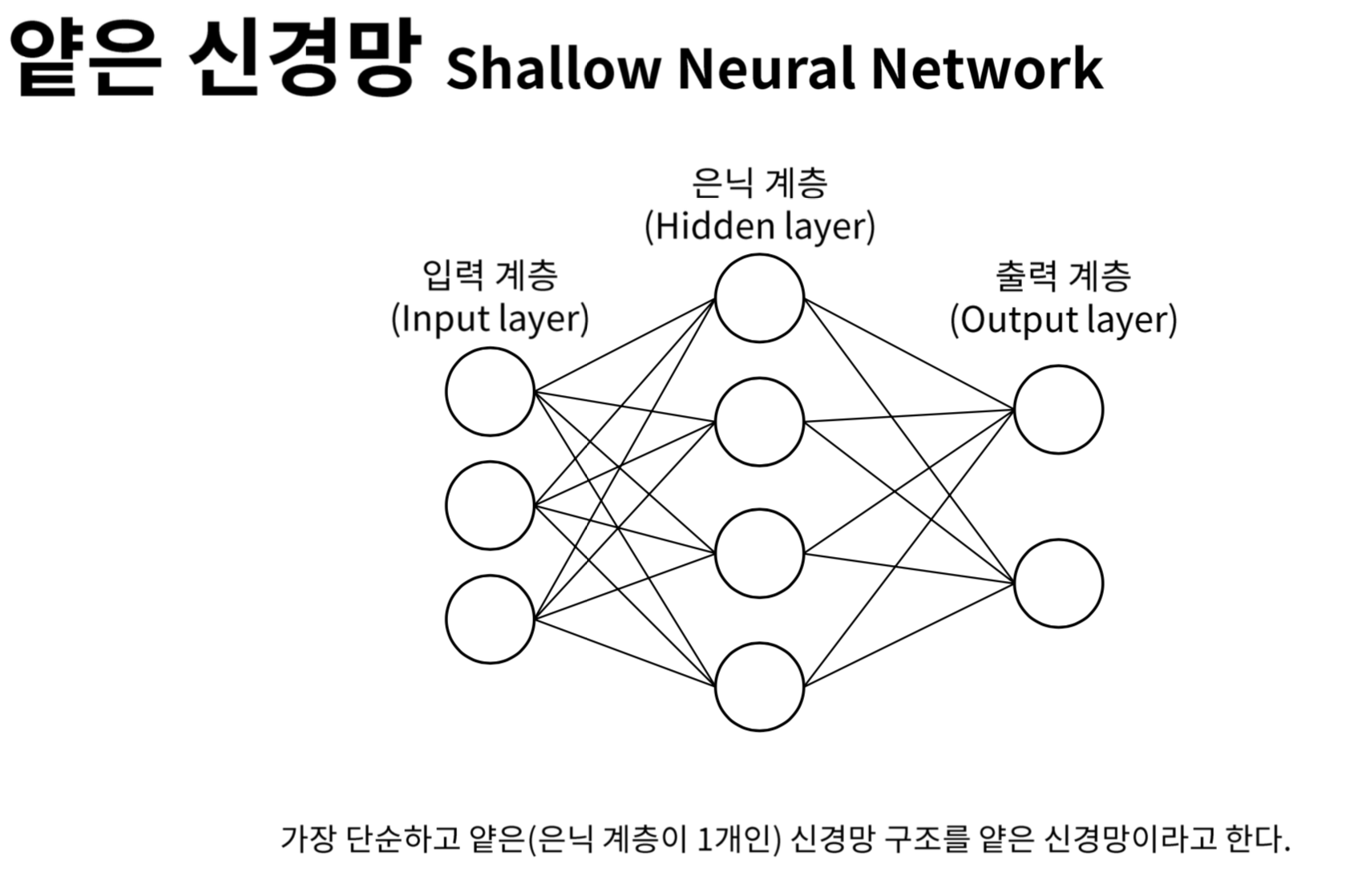
은닉층(Hidden layer)이 하나뿐인 얕은 신경망(Shallow layer)입니다. 왠지 모르게 “얕은 신경망”이라는 이름이 붙어 있지만 그냥 은닉층 1단짜리 심층 신경망입니다. 왜 이런 이름이 있지? 제 생각이지만 은닉층 1층짜리밖에 구현 못하던 시절엔 이걸 심층 신경망이라 불렀는데 더 깊게 구성할 수 있는 기술이 개발된 후 진짜 심층 신경망과 구분하기 위해 지은 이름이 아닐까요? 제 생각일 뿐이니 한귀로 듣고 한귀로 흘리시길 바랍니다….
다음 그림은 위의 얕은 신경망에서 발전된 형태인 진짜배기 심층 신경망입니다.
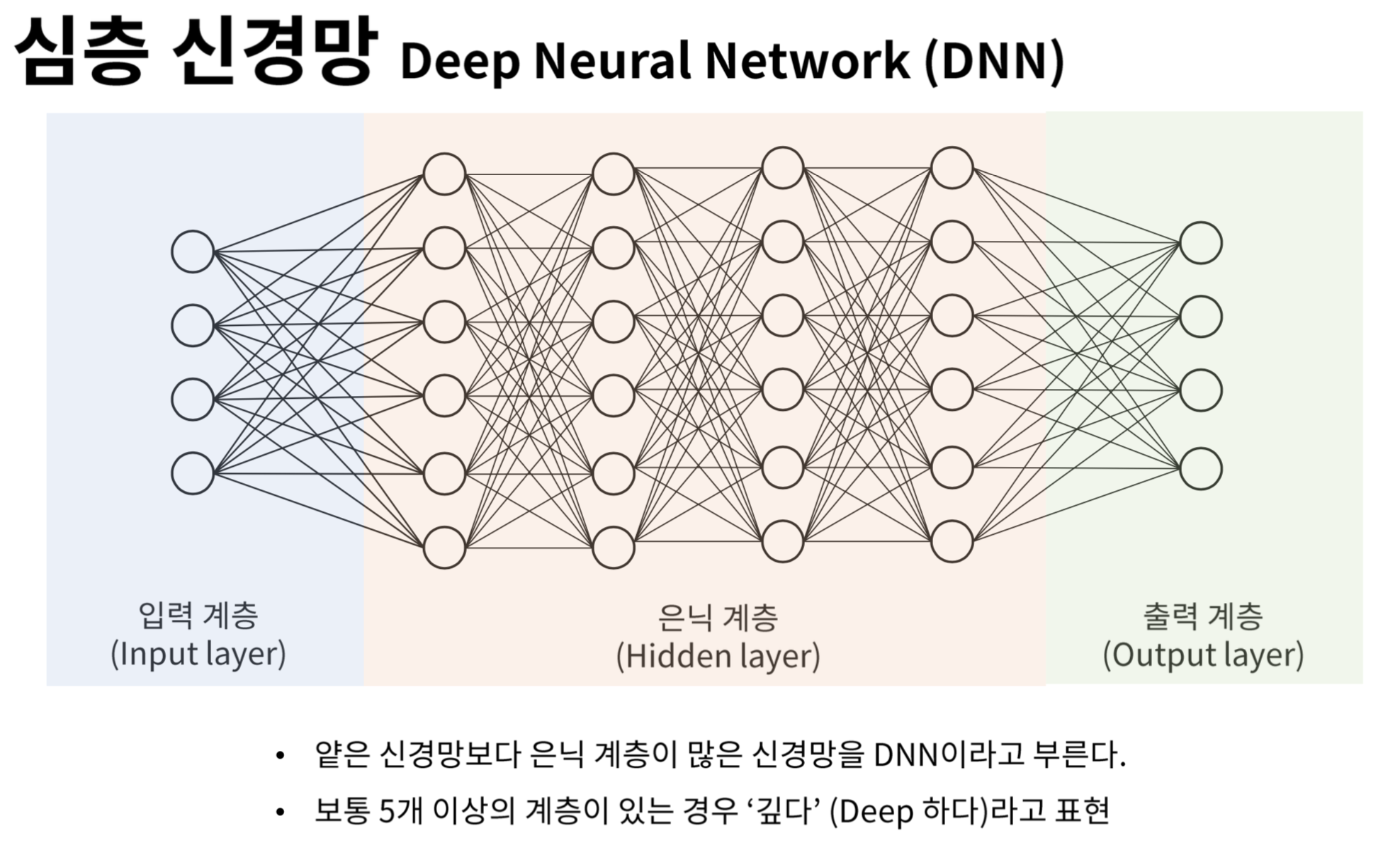
이런 식으로 다수의 뉴런으로 심층 신경망을 구현하여 가중치를 구할 수 있습니다.
과적합 방지법
과적합은 훈련 데이터에 모델이 과도하게 회귀되어 오히려 실제 사용에서 성능이 떨어지는 현상입니다. 훈련 데이터에 대한 노이즈까지 학습을 해버려서 일어나는 현상인데, 훈련 데이터에서는 높은 정확도를 보이지만 검증 데이터나 테스트 데이터에서는 제대로 동작하지 않습니다. 이러한 현상을 방지할 수 있는 방법에 대해서 정리하였습니다.
1. 데이터 양을 늘리기
과적합 뿐만 아니라 모델 자체의 성능을 높이는 데도 좋은 방법입니다. 심층 신경망 구조는 학습시킬 데이터가 많을수록 정확도가 올라가는 성질, 즉 데이터의 일반적인 패턴을 학습시키는 방법이라고 볼 수 있습니다. 노이즈가 있는 데이터와 없는 데이터를 모두 학습하며 모델이 좀 더 견고해지는 효과를 볼 수 있습니다.
하지만 데이터가 항상 충분할 수는 없으므로 의도적으로 데이터를 변형하여 더 많은 학습 데이터를 생성하기도 하는데, 이를 데이터 증식 또는 증강(Data Augmentation)이라고 합니다. 이미지를 돌리거나 자르고, 노이즈를 추가하거나 밝기를 낮추는 식으로 데이터 갯수를 부풀리는 식의 방법입니다.
2. 데이터 정규화
데이터 정규화에는 $L1$ 정규화와 $L2$ 정규화가 있습니다. 이에 따라 필요한 용어부터 살펴보도록 하겠습니다.
$L1$ Norm & $L2$ Norm
$L1$ 정규화와 $L2$ 정규화를 설명하기에 앞서 $L1$, $L2$ Norm에 대해서 설명하겠습니다. 우선 Norm이란 것은 벡터의 거리를 측정하는 방법입니다. 이를 표현한 수식은 다음과 같습니다.
$\left \| x \right \|_p:=\left (\sum_{i=1}^{n}\left | x_i \right |^p\right )^{1/p}$
이때 p값은 Norm의 차수를 의미합니다. $L1$, $L2$에 있는 숫자가 바로 p입니다. 이 공식에 따르면 $L1$ Norm과 $L2$ Norm은 다음과 같습니다.
$p=(p_1, p_2, \cdots, p_n), q=(q_1, q_2, \cdots, q_n)$ 일 때,
$L1\;Norm: \; \left \| x \right \|_1=\sum_{i=1}^{n}\left | p_i-q_i \right |$
$\begin{align*} L2\;Norm: \;\left \| x \right \|_2&=\left (\sum_{i=1}^{n}\left | p_i-q_i \right |^2\right )^{1/2} \\
&= \sqrt{(p_1-q_1)^2+(p_2-q_2)^2+\cdots+(p_n-q_n)^2}
\end{align*}$
$L1$ Norm은 각 $p,q$원소들 간의 직선거리입니다. $L2$ Norm은 $p, q$ 벡터 사이의 직선거리입니다.
$L1$ Loss & $L2$ Loss
이러한 방식으로 $L1$ Loss와 $L2$ Loss 함수를 구현할 수 있습니다. $p$ 벡터를 실제 값으로, $q$ 벡터를 예측치로 치환하면 두 식은 다음과 같습니다.
$L1\;Loss=\sum_{i=1}^{n}\left | y_i-f(x_i) \right |$
$L2\;Loss=\sum_{i=1}^{n}\left ( y_i-f(x_i) \right )^2$
$L1$ Loss와 $L2$ Loss의 차이는 잘못된 값에 대해서 $L2$ Loss의 경우 오차의 제곱을 더해 주기 때문에 $L2$ Loss가 Outlier에 더 민감하다는 점입니다. 따라서 Outlier가 적당히 무시되길 원하면 $L1$ Loss를 사용하고, Outlier의 등장에 신경써야 한다면 $L2$ Loss를 사용하는 것이 좋습니다.
$L1$ Regularization & $L2$ Regularization
위의 Loss 함수를 원래 모델에서 사용하던 Cost 함수에 추가하면 다음과 같은 결과를 얻을 수 있습니다.
$L1\;Regularization:\;\; cost(W,b)=\frac{1}{n} \sum_{i=1}^{n} \left \{ L(y_i,\hat{y_i})+\frac{\lambda}{2}\left | w \right |\right \}$
$L2\;Regularization:\;\; cost(W,b)=\frac{1}{n} \sum_{i=1}^{n} \left \{ L(y_i,\hat{y_i})+\frac{\lambda}{2}\left | w \right |^2\right \}$
$L(y_i,\hat{y_i}):$ 기존의 Cost function
기존의 오차함수에 가중치의 크기가 포함되면서 가중치가 너무 큰 방향으로 학습되지 않도록 하는 항을 추가해 주었습니다. 이때 $\lambda$는 학습률로 정규화의 효과를 조절하는 항으로 사용됩니다.
$L1$ Regularization과 $L2$ Regularization의 차이는 $L2$ Regularization는 미분이 가능하여 Gradient-based learning이 가능하다는 점입니다.
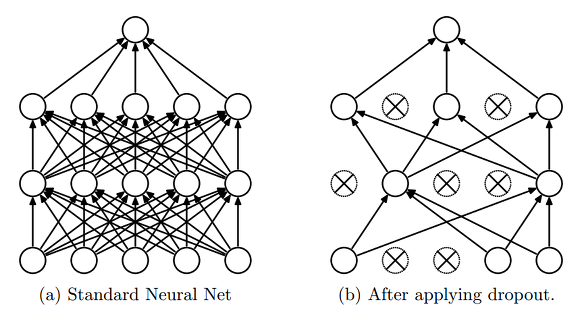
3. Dropout
Dropout은 의도적으로 은닉층의 일정 비율을 일부러 학습하지 않아 새로운 Epoch마다 조금씩 특징이 다른 데이터 셋을 학습시키는 효과를 내는 방법입니다. 여러 개의 모델을 만들지 않고도 모델 결합이 여러 형태를 가지게 하는 것입니다. 네트워크를 학습하는 동안 랜덤하게 일부 유닛이 동작하는 것을 생략한다면 뉴런의 조합만큼 지수함수적으로 다양한 모델을 학습시키는 것과 같습니다. n개의 유닛이 있다고 하면 $2^n$개 만큼의 모델이 생성될 것입니다.
마무리
이번 게시글에서는 DNN과 과적합을 방지하는 법에 대해서 정리했습니다. 다음 게시글은 Convolution Nerual Network과 LeNet에 대해서 정리하겠습니다.
질문
- 은닉층을 Wide하게 만드는 것보다 Deeper하게 만드는 것이 좋은 이유가 무엇인가요? 모델이 자연스럽게 계층 구조를 가지게 된다는 의미를 잘 모르겠습니다. 계층별로 비슷한 녀석들끼리 모인다는 뜻인가요?
보충
1) 다층 신경망(Multi-layer Perceptron)이라고도 함
참고 사이트
Udacity Self-driving car nanodegree - Deep Nerual Network(링크 공유 불가능)
답을 찾아가는 과정 - “딥러닝 - 활성화 함수(Activation) 종류 및 비교”
DataLatte’s IT Blog - “심층 신경망의 구조”
Refstop
Deep Learning 및 SLAM을 공부하고 있습니다.








Comments