지난 게시글들에서는 뉴럴 네트워크를 활성화 함수에 따라 이산 모델, 연속 모델로 나누어서 살펴보았습니다. 뉴럴 네트워크의 최종 목적은 정확한 예측 모델, 선형 함수를 만드는 것입니다. 이 선형 함수를 이산 모델에서는 Step Function, 연속 모델에서는 Sigmoid 또는 Softmax 함수에 대입합니다. 그 후 이산 모델에서는 퍼셉트론 알고리즘으로 가중치를 조절, 연속 모델에서는 Cross-Entropy 오차함수와 경사하강법을 사용하여 가중치를 조절합니다. 그 결과, 뉴럴 네트워크의 예측 모델인 선형 함수를 도출할 수 있습니다.
이번 게시글에서는 비선형 모델에 대해서 알아보겠습니다. 비선형 모델은 어떤 식으로 찾을 수 있을까요? 바로 선형 함수를 여러개 합치는 것입니다. 간단한 예시를 보겠습니다.
지난 게시글들에서는 뉴럴 네트워크를 활성화 함수에 따라 이산 모델, 연속 모델로 나누어서 살펴보았습니다. 뉴럴 네트워크의 최종 목적은 정확한 예측 모델, 선형 함수를 만드는 것입니다. 이 선형 함수를 이산 모델에서는 Step Function, 연속 모델에서는 Sigmoid 또는 Softmax 함수에 대입합니다. 그 후 이산 모델에서는 퍼셉트론 알고리즘으로 가중치를 조절, 연속 모델에서는 Cross-Entropy 오차함수와 경사하강법을 사용하여 가중치를 조절합니다. 그 결과, 뉴럴 네트워크의 예측 모델인 선형 함수를 도출할 수 있습니다.
이번 게시글에서는 비선형 모델에 대해서 알아보겠습니다. 비선형 모델은 어떤 식으로 찾을 수 있을까요? 바로 선형 함수를 여러개 합치는 것입니다. 간단한 예시를 보겠습니다.
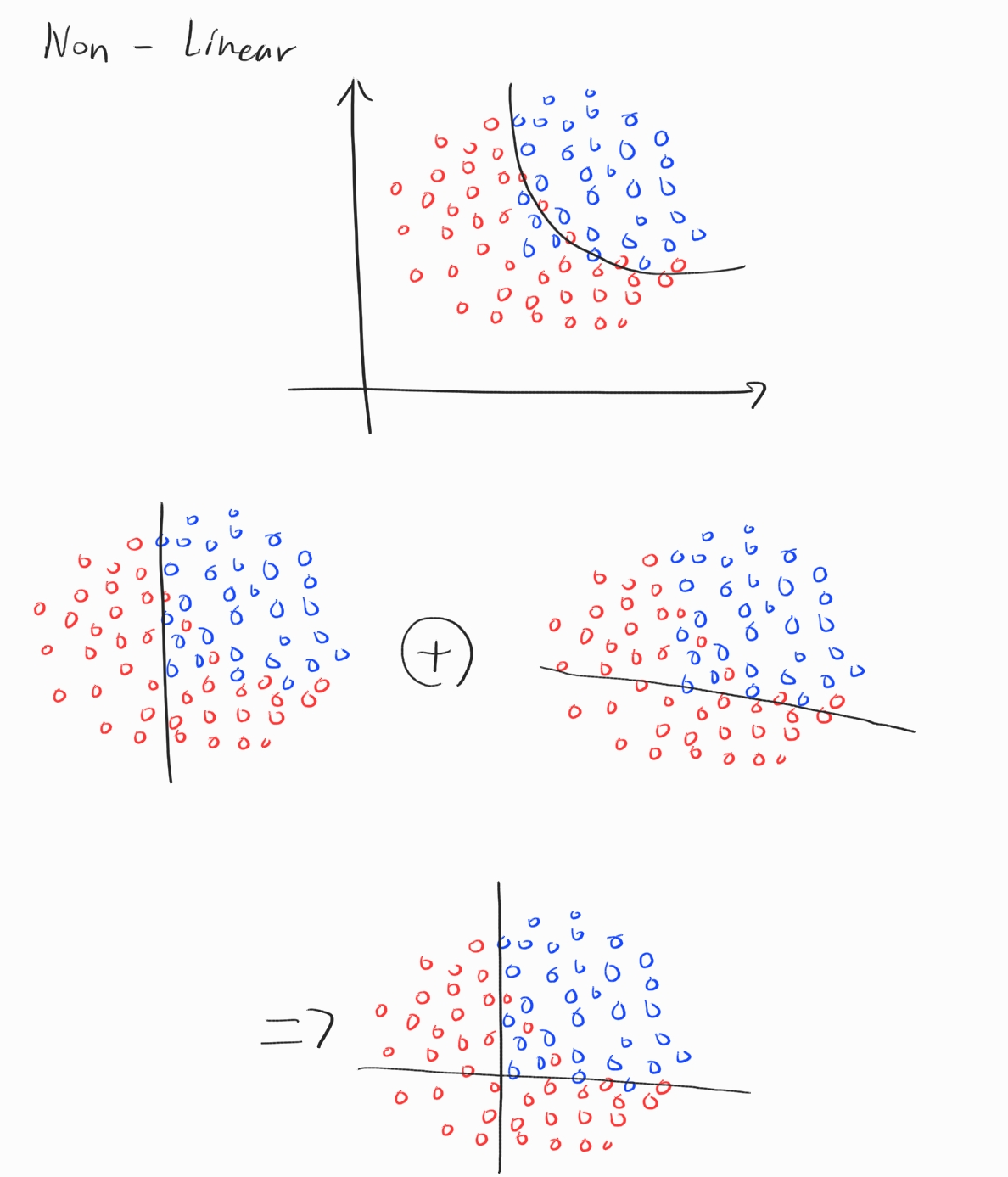
위의 그림은 두 선형 함수를 합쳐서 비선형 함수를 만들어내는 과정입니다. 이 과정을 노드 그래프로 나타내면 다음과 같습니다.
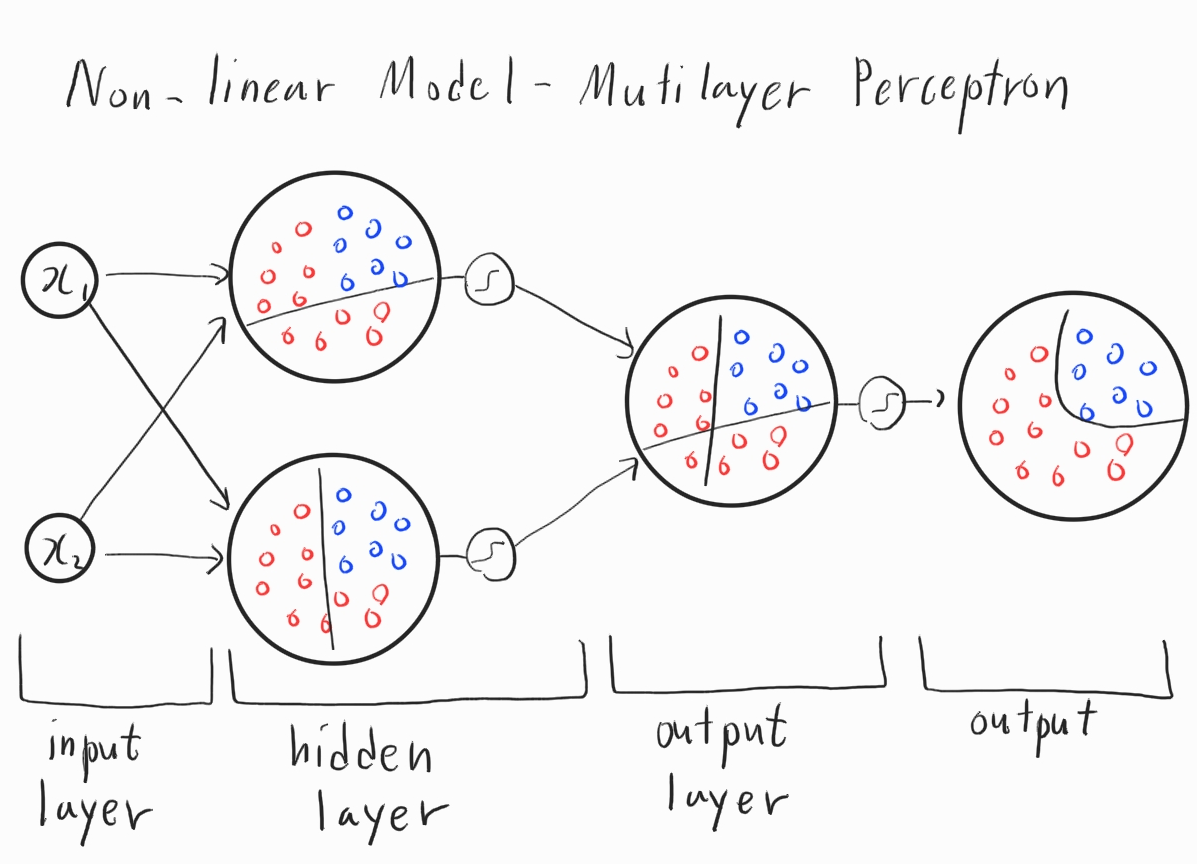
맨 좌측부터 입력층, 은닉층, 출력층으로 이루어져 있습니다. 이렇게 입력층과 출력층 외의 은닉층이 존재하는 뉴럴 네트워크를 다층 신경망이라고 합니다. 사실 은닉층이라고 해도 하는 일은 똑같습니다. 입력층의 입력을 받아 선형모델의 결과를 활성화 함수에 대입하여 은닉층의 결과를 도출합니다. 다시 은닉층의 결과값을 출력층에 대입하여 나온 출력이 바로 비선형 모델의 결과물입니다. 물론 여기서 추측할 수 있는 점은 입력이 $x_1, x_2, \cdots , x_n$과 같이 많아지면 많아질수록 출력이 나오기까지, 즉 결과가 분류되기까지 은닉층이 많아질 것입니다. 그렇다면 점점 더 복잡한 비선형 함수를 학습할 수 있게 됩니다.
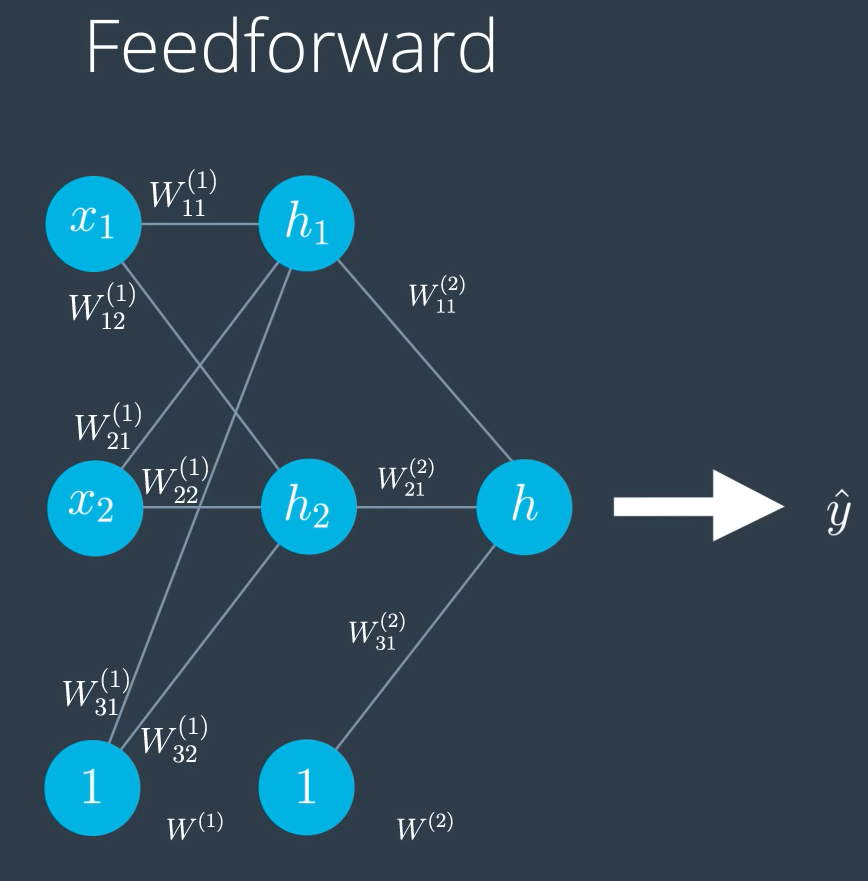
이때 비선형 모델의 결과를 내는 과정을 순전파라고 합니다. 순리를 거스르지 않고 입력층부터 은닉층을 거쳐 출력층에서 출력을 내보냅니다. 위의 비선형 모델 다층 신경망 그림에 나온 과정을 그대로 따라갑니다.
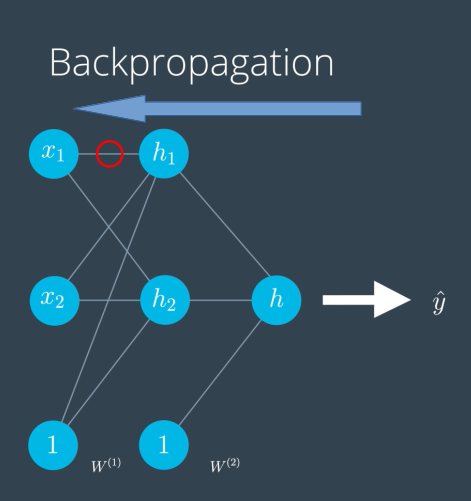
역전파는 순전파와 반대로 출력값으로부터 입력값 방향으로 계산하여 가중치 조정값을 찾는 과정을 의미합니다. 저번 게시글에서 봤던 경사 하강법과는 다르게 다층 신경망에서 오차함수의 미분을 구할 때 사용하는 방법입니다. 오차함수를 가중치로 미분한 값의 의미는 이 가중치가 오차에 얼마나 영향을 미치는가입니다. 저번과 마찬가지로 수정할 가중치에 대해 연쇄법칙을 사용하여 그 가중치가 영향을 미치는 노드들을 출력 쪽에서부터 되짚어 가면서 오차의 미분을 구합니다. 위의 그림에 표시된 가중치는 $W^{(1)}{11}$입니다. 이 가중치에 대한 오차의 미분값을 계산해 보겠습니다. 오차함수를 $E(W)$로 표현하면, 오차를 가중치 $W^{(1)}{11}$에 대하여 미분한 값은 $\large{\frac{\partial E}{\partial W^{(1)}_{11}}}$입니다. 이 미분값을 연쇄법칙을 사용하여 나타낸 값은 다음과 같습니다.
연쇄법칙한 결과의 각 항은 경사 하강법 때 계산했던 방식과 같은 방법으로 구할 수 있습니다.
이번 강의에서 배운 뉴럴 네트워크는 여기까지입니다. 다음에 정리할 내용은 Tensorflow의 사용에 대해 정리해 보겠습니다.
Udacity Self-driving car nanodegree - Neural Network(링크 공유 불가능)
Comments