Neural Network란?
뉴럴 네트워크는 우리말로 신경망이라는 의미입니다. 옛날 옛적 공학자들은 컴퓨터에 지능, 즉 학습능력을 부여할 방법을 고민했고, 결국 사람의 뇌 구조를 모방하는 방법을 고안했습니다. 우리 뇌 속의 뉴런 세포가 연결 및 신호를 주고받는 방식을 알고리즘으로 구현하여 신경망이라는 것을 만들었습니다.
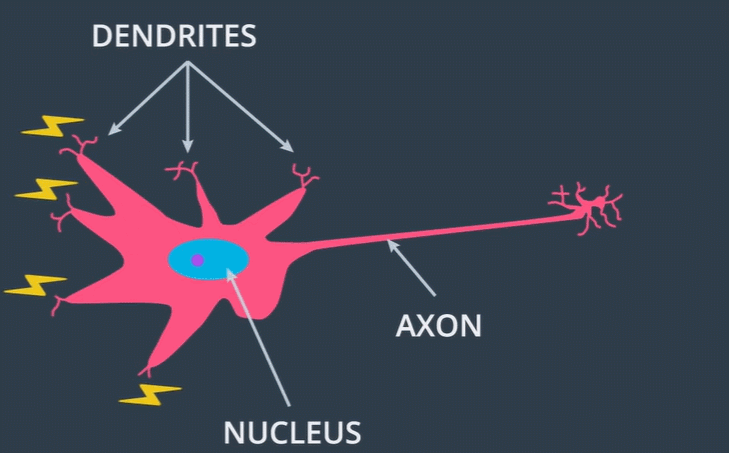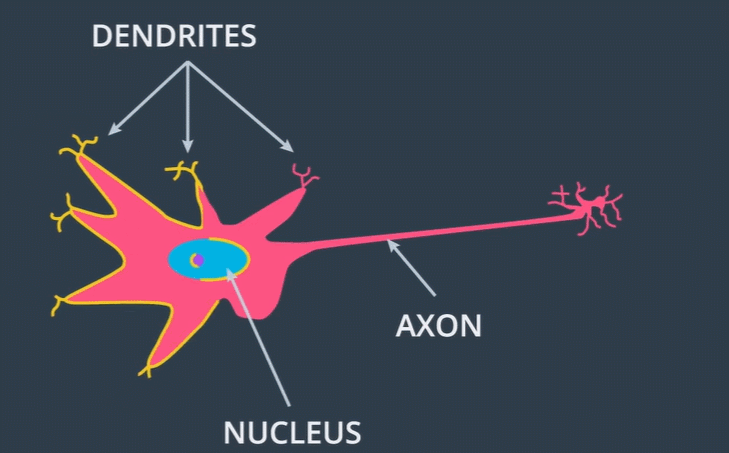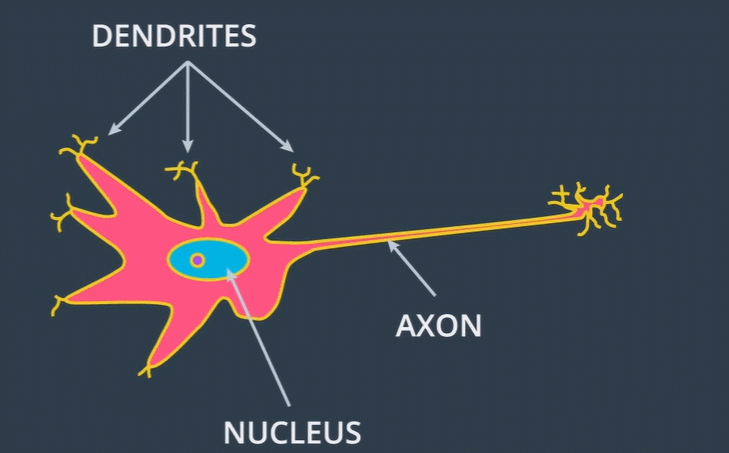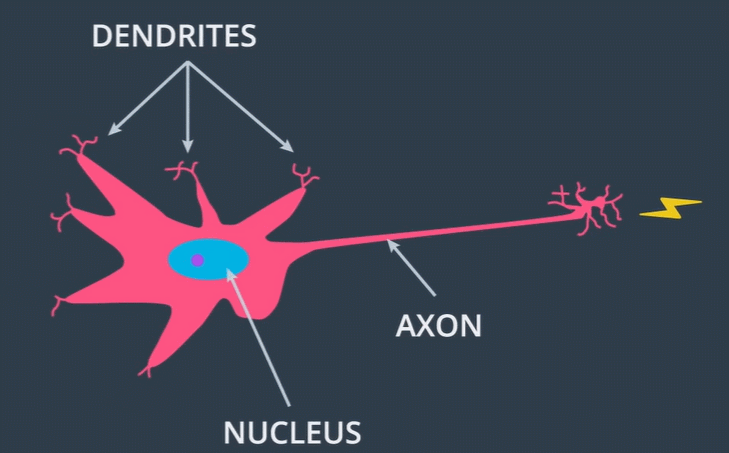
위 그림을 보면 뉴런 세포의 가지돌기(Dendrite)로 전기 신호가 전달되어 핵(Nucleus)을 통해 축삭(Axon)으로 전기 신호가 나갑니다. 지금부터 이러한 뉴런의 구조를 어떻게 구현했는지 알아볼 것입니다.
선형 회귀 (Linear Regression)
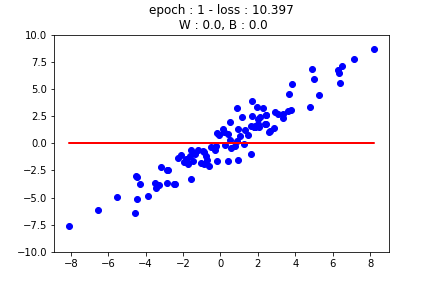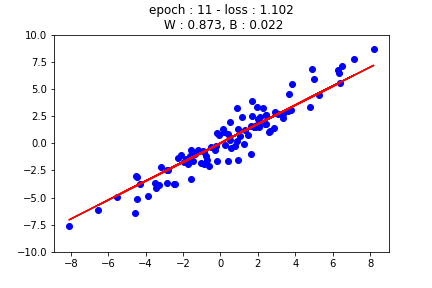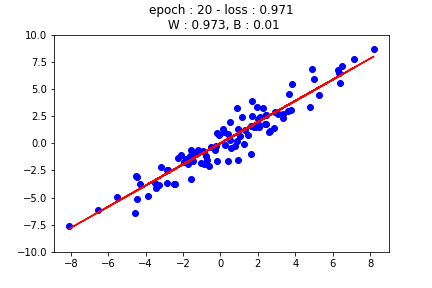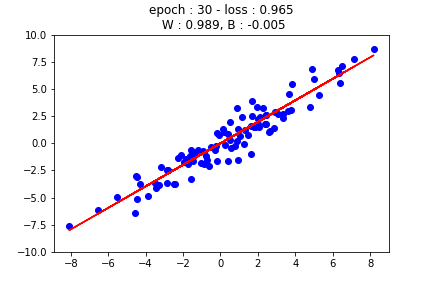
먼저 가장 기초적인 선형 회귀를 살펴보겠습니다. 선형 회귀란 자료가 분포한 형태를 보고 $x$축과 $y$축 사이의 샘플 관계를 선형으로 나타내는 방법입니다. 일반적으로 선형 회귀 모델의 형태는 다음과 같습니다.
$\large{
w_1x_1+w_2x_2+b=0
}$
위의 공식에서는 가중치가 $w_1$, $w_2$ 둘 뿐이지만 실제로는 고려해야 할 가중치 수만큼 필요합니다. 데이터의 수가 $n$개라면, 그 수인 $n$개만큼 가중치가 존재합니다. 데이터와 가중치를 표현하면 다음과 같습니다.
$\large{
X=\begin{bmatrix}
x_1 \\
x_2 \\
\vdots \\
x_n
\end{bmatrix}
\;\;\;\;\;\;\;\;\;
W=\begin{bmatrix}
w_1 \\
w_2 \\
\vdots \\
w_n
\end{bmatrix}
}$
바이어스는 그냥 $b$로 선형 모델당 하나입니다. 이들을 행렬로 된 식으로 나타내면 다음과 같습니다.
$\large{
WX+b=0
}$
하지만 이 강의에서는 이해를 돕기 위해서 2개의 가중치만 사용할 것입니다. 위의 그림에서 볼 수 있듯이 가중치와 바이어스 수정을 통해 선형 회귀 모델을 찾게 됩니다.
로지스틱 회귀 (Logistic Regression)
로지스틱 회귀는 회귀를 사용하여 데이터가 어떤 범주에 속할 확률을 0에서 1 사이의 값으로 예측하고, 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류해주는 지도 학습 알고리즘입니다. 핵심은 분류입니다. 회귀라고 부르지만 정작 기능은 분류인 이상한 녀석입니다. 이 이름의 유래는 연속형 변수 대신 범주형 변수에 회귀시키려다 발생한 문제입니다.
로지스틱 회귀를 사용하는 이유
첫번째 예시는 나이에 따른 혈압의 증가 데이터입니다. 그래프를 보면 선형 회귀가 잘 이루어진 것을 볼 수 있습니다.
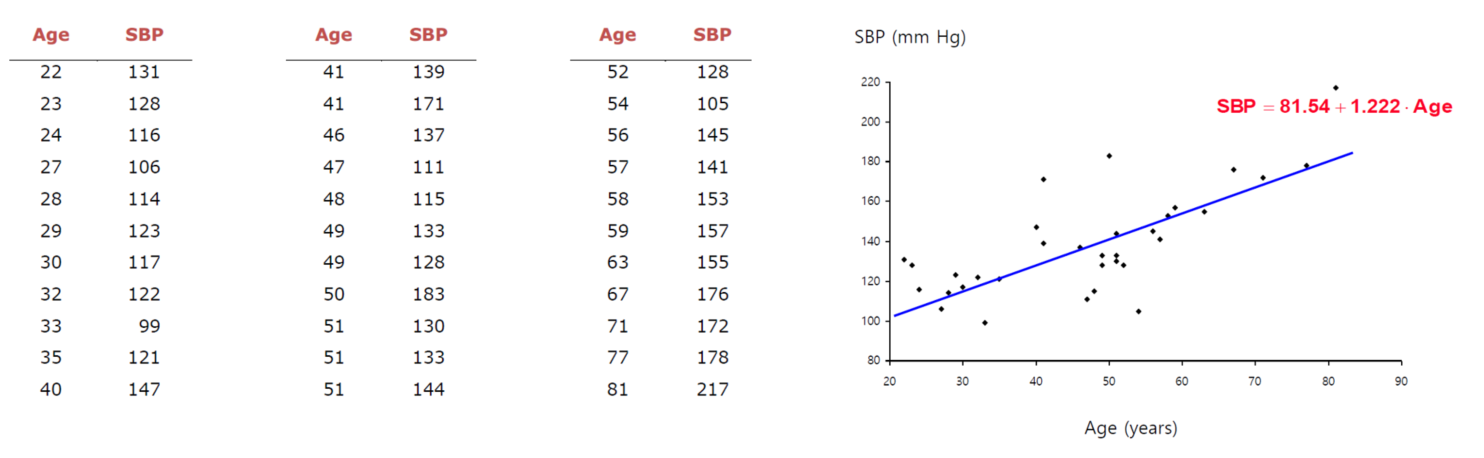
두번째 예시는 나이에 따른 암 발생 여부 데이터입니다. 데이터 결과값이 yes or no, 즉 0과 1로 출력됩니다. 데이터의 경향을 잘 따르는 첫번째 그래프와는 달리 이번 그래프는 뭔가 이상합니다.
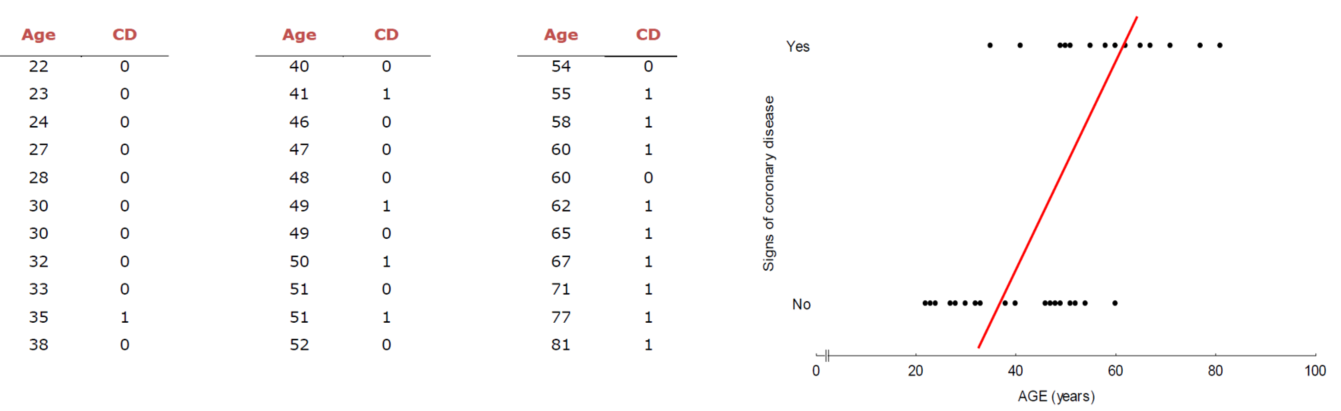
결과값이 0~1 사이의 값이 나와야 하는데 양의 무한대, 음의 무한대까지 올라가 버립니다. 이것이 범주형 변수에 선형회귀를 적용했을 때의 문제입니다.
이제 어떤 방식으로 이 문제를 해결할 수 있는지 봅시다.
로지스틱 회귀의 개요
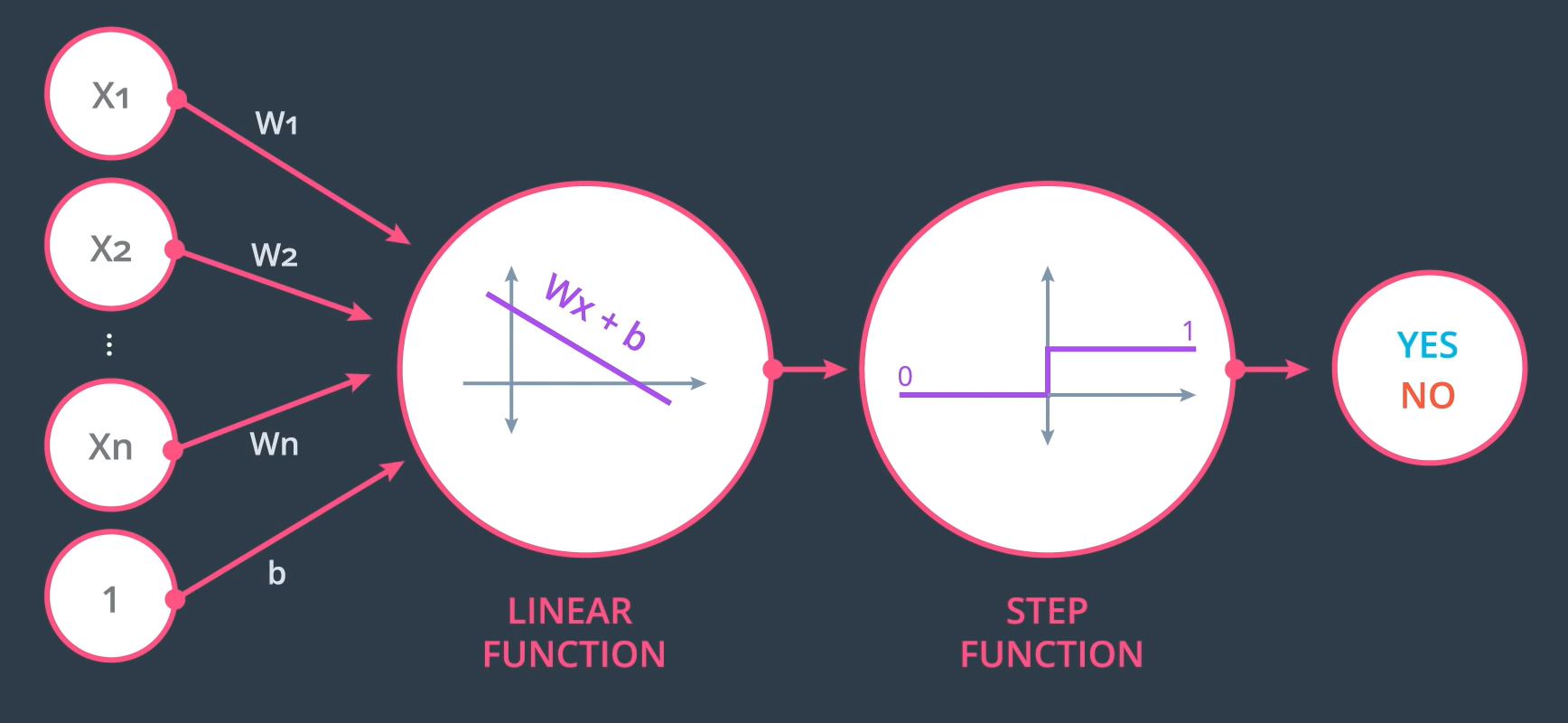
로지스틱 회귀가 선택한 해결방법은 바로 활성화 함수(Activation Function)를 사용하는 것입니다. 활성화 함수는 선형 모델을 비선형 모델로 만들어 주는 역할을 하고 있습니다. 선형 모델만 다층으로 쌓을 경우, 결국 결과가 선형 모델이 되는 문제점이 있기에, 비선형 함수를 한번 거쳐주는 과정이 필요합니다. 로지스틱 회귀에서 주로 사용되는 활성화 함수는 Step, Sigmoid, Softmax 함수입니다. 이 함수들은 어떤 *모델에서 적용하는지에 따라, 그리고 분류할 범주의 갯수에 따라 사용 함수가 다릅니다. 모델에 따라서는 Step Function은 이산 모델에서 사용하고, Sigmoid와 Softmax는 연속 모델에서 사용합니다. 또한 범주에 따라서는 범주가 2개(일반적으로 0 또는 1, yes or no 같은것)일 때 Step Function과 Sigmoid, 3개 이상일때 Softmax를 사용합니다. 이 함수들에 대해서는 앞으로 더 자세히 알아보도록 하겠습니다.
선형 경계면 (Linear Boundary)
계속해서 로지스틱 회귀를 알아보겠습니다. 다음의 자료는 학생들의 시험 시행 횟수에 따른 평균 등급을 샘플로 나타낸 것입니다.
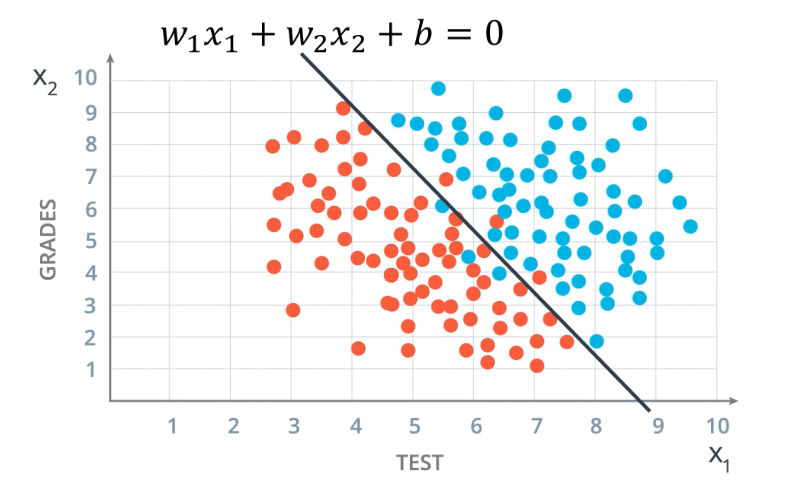
시험 횟수가 많을수록, 그리고 성적이 높을수록 Pass 범주로, 시험 횟수가 적을수록, 그리고 성적이 낮을수록 Fail 범주로에 분류됩니다. 음… 그런데 시험 횟수가 적고 등급이 높은 사람은 불합격은 횟수가 걸릴 수 있으니 불합이 될 수 있지만, 시험 횟수가 많은데 등급이 낮은 사람은 합격이라… 이 결과는 뭔가 이상하네요. 아무튼 분류의 예시를 드는데는 문제가 없으니 이 데이터를 예시로 들겠습니다. 이 그림을 관찰해 보면 $w_1x_1+w_2x_2+b=0$의 선형 모델로 Pass와 Fail을 구분할 수 있습니다. 따라서 데이터를 선형 모델에 대입했을 때 $w_1x_1+w_2x_2+b$의 값이 0 이상이면, 즉 0이거나 양수이면 Pass, 0 이하, 즉 음수이면 Fail로 분류할 수 있습니다. 이때 Pass를 1, Fail을 0이라는 값을 부여한다고 하면 출력값, 결과 $y$의 함수는 다음과 같습니다.
$\large{
y=\left\{\begin{matrix}
0\;\;\;\;if\;w_1x_1+w_2x_2+b<0\\
1\;\;\;\;if\;w_1x_1+w_2x_2+b\geq 0
\end{matrix}\right.
}$
이 $y$의 함수를 그래프로 나타낸 것이 바로 Step Function입니다. 간단히 말해서 양수일때 1, 음수일때 0의 결과를 도출하는 함수입니다. 이산 모델에선 이 함수를 활성화 함수로 사용하게 됩니다.
Perceptron Algorithm
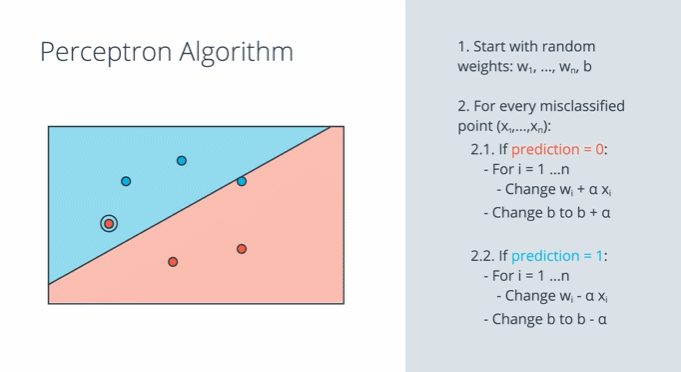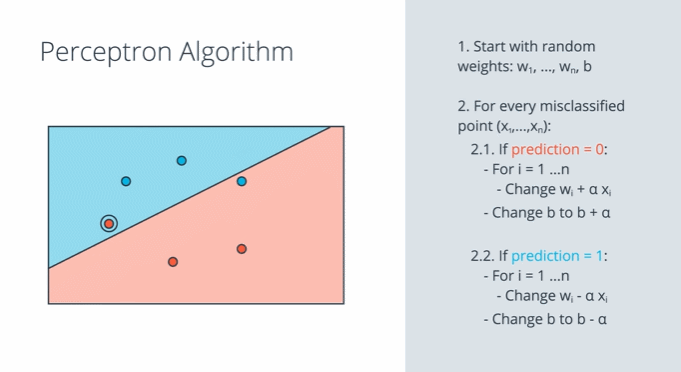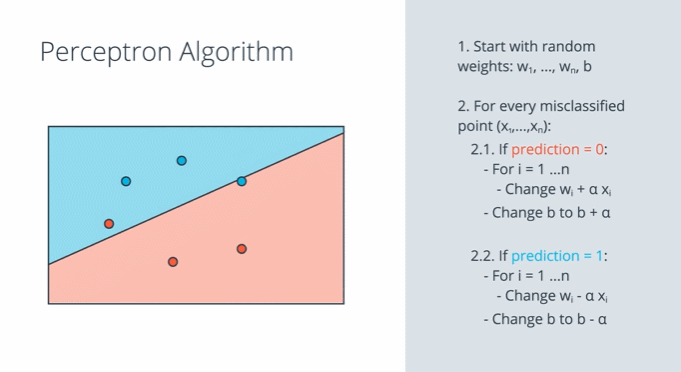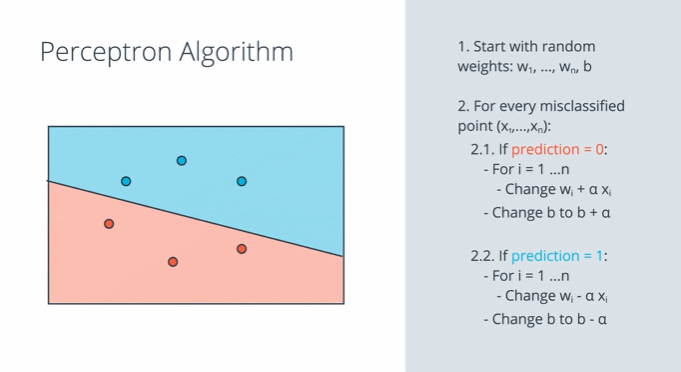
퍼셉트론 알고리즘은 가중치와 바이어스를 조정해 주는 알고리즘입니다. 잘못 분류된 sample의 성분을 현재 선형 모델에 적용하여 가중치 $w_1, w_2$와 바이어스 $b$를 보정해 줍니다. 하지만 한번에 그 sample의 성분만큼 조정하면 가중치와 바이어스의 변화가 너무 급격하기 때문에 학습률 $\alpha$로 반영 비율을 조정합니다. 이 과정을 잘못 분류된 모든 샘플에 대하여 시행합니다.
이 알고리즘이 반복되는 동안 선형 모델은 잘못된 sample에 점점 더 가까이 접근합니다. 결국 과정이 끝나고 나면 위 그림의 마지막과 같이 잘못된 sample을 분류하게 됩니다.
마무리
이산 모델의 선형 모델 찾는 방법은 여기까지입니다. 선형 모델을 찾은 후, 활성화 함수에 대입하여 0 또는 1의 결과를 구합니다. 다음 게시글에서는 이산 모델에서 연속 모델로 변화했을 때 추가되는 과정들을 알아보겠습니다.
질문
- 딥러닝 방식, 즉 다층 신경망을 사용하는 방법은 모두 이런 방식인가요?
- *이산 모델, 연속 모델이라고 사용하는게 맞나요?
- Positive면 (–)해주고 negative면 (+)해주는 이유가 뭔가요?
- 가중치에 sample값을 반영하여 가중치를 수정할 수 있는 이유? 가중치와 sample(x1 x2)의 관계?
- 가중치를 초기화해줄 수 있는 방법은 없나요?
참고 사이트
Udacity Self-driving car nanodegree - Neural Network(링크 공유 불가능)
Refstop
Deep Learning 및 SLAM을 공부하고 있습니다.









Comments