이미지의 개체 식별법

카메라 캘리브레이션, 왜곡 교정, 원근 변환 등으로 보정된 이미지에서 어떤 개체, 예를 들면 차선 같은 개체를 찾아내는 방법에 대해서 알아보겠습니다. 컴퓨터가 이미지에서 개체를 식별하는 방법의 키워드는 그래디언트(Gradient)입니다. 그래디언트는 경도, 기울기, 변화도 등으로 해석될 수 있습니다. 이전의 색상과 비교하여 다음 색상과의 색상값 차이(RGB)를 계산하여, 변화가 크면 변화도가 큰 것으로, 물체의 경계(edge)라고 판단합니다. 이번 게시글에서는 그래디언트 계산 방법 중 Sobel 필터에 대해서 정리합니다.

Sobel Filter(Sobel Mask)

소벨 필터는 위에서 언급했듯이 물체의 경계를 찾는 필터입니다. 생김새는 다음과 같습니다.

$\large{ sobel_x=\begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix}\;\;\;\;\;\;\;\;\; sobel_y=\begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix} }$

$sobel_x$는 수직 성분 검출, $sobel_y$는 수평 성분 검출 필터입니다. 이는 에지 검출의 대표적인 1차 미분 연산자인데, 미분 연산자라는 말이 조금 이해하기 힘들 수 있습니다. 그럼 먼저 미분 연산자에 대해서 알아봅시다.

1차 미분 연산자

미분 연산자라고 불리는 이유는 소벨 필터는 변화도를 이용하기 때문입니다. 1차 미분 연산자란 다음과 같습니다.

$\large{ \begin{align*} \frac{\partial f}{\partial x}&=\frac{f(x+1)-f(x)}{x+1-x}\\ &=f(x+1)-f(x)\\ &=\begin{bmatrix} -1 & 1 \end{bmatrix}\; \begin{bmatrix} f(x+1) \\ f(x) \end{bmatrix} \end{align*} }$

즉, 미분 연산자만 따로 보면 다음과 같습니다.

$\large{ \frac{\partial }{\partial x}\times f=\begin{bmatrix} -1 & 1 \end{bmatrix}\; \begin{bmatrix} f(x+1) \\ f(x) \end{bmatrix} }$ $\large{ \frac{\partial }{\partial x}=\begin{bmatrix} -1 & 1 \end{bmatrix} }$

그렇다면 $x+1$부터 $x-1$의 변화량을 봅시다. 어차피 기울기의 크기를 보는거라 분모는 별로 중요하지 않기 때문에 분자만을 나타내면 다음과 같습니다.

$\large{ \begin{align*} \frac{\partial f}{\partial x}&=f(x+1)-f(x-1)\\ &=\begin{bmatrix} -1 & 0 & 1 \end{bmatrix}\; \begin{bmatrix} f(x+1) \\ f(x) \\ f(x-1) \end{bmatrix} \end{align*} }$ $\large{ \frac{\partial }{\partial x}=\begin{bmatrix} -1 & 0 & 1 \end{bmatrix} }$

1$\times$3 마스크는 다음과 같습니다. 소벨 필터는 보통 차원이 홀수인 n$\times$n 정방행렬로 되어 있는데, 이는 *검출할 라인을 제외하고 미분 연산자를 곱해주기 때문입니다. 위에서 언급한 소벨 필터의 생김새 역시 3$\times$3 행렬입니다.

소벨 마스크

이런 식으로 1$\times$3 1차 미분 연산자 3개를 3$\times$3 행렬로 만든 것을 Prewitt Masks라고 합니다. 소벨 마스크가 되기 전 단계입니다. 생김새는 다음과 같습니다.

$\large{ sobel_x=\begin{bmatrix} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \end{bmatrix}\;\;\;\;\;\;\;\;\; sobel_y=\begin{bmatrix} -1 & -1 & -1 \\ 0 & 0 & 0 \\ 1 & 1 & 1 \end{bmatrix} }$

깔끔하게 3개의 1차 미분 연산자로 만들어져 있습니다. 이 프리윗 마스크를 조금 수정하여 중심화소에 조금 가중치를 둔 것이 바로 Sobel Mask입니다. 중심화소에 가중치를 크게 함으로서 대각선 방향에서의 에지도 잘 검출합니다.

$\large{ 수직\;방향\;검출:\;sobel_x=\begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix}\;\;\;\;\;\;\;\;\; 수평\;방향\;검출:\;sobel_y=\begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix} }$ $\large{ 대각선\;방향\;검출:\;sobel_d=\begin{bmatrix} 0 & -1 & -2 \\ 1 & 0 & -1 \\ 2 & 1 & 0 \end{bmatrix} }$

소벨 필터로 Gradient 구하기

이제 소벨 필터로 그래디언트를 구해 봅시다. 그래디언트를 구하는 방법은 간단합니다. 먼저 3$\times$3 이미지 픽셀에 소벨 마스크의 각각의 요소들을 곱합니다. 그리고 결과의 모든 요소의 합이 바로 그래디언트입니다. 식으로 나타내면 다음과 같습니다.

$\large{ gradient=\sum (region\times Sobel\;mask) }$

이 그래디언트 값은 3$\times$3 이미지 픽셀의 중심에서의 그래디언트 값으로 취급합니다. 이제 gradient를 구했으니, 예제를 한번 해 보도록 합시다.

Sobel Filter 예제

소벨 필터를 사용하는 예제는 다음과 같습니다.

import cv2
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg

img = mpimg.imread('/home/이미지 경로/sobel_ex.png')
gray = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
# Sobel(이미지, 이미지 비트 수, x축, y축)
sobelx = cv2.Sobel(gray, cv2.CV_64F, 1, 0)
sobely = cv2.Sobel(gray, cv2.CV_64F, 0, 1)
# Gradient를 모두 양수로 변환, 절댓값을 본다.
abs_sobelx = np.absolute(sobelx)
abs_sobely = np.absolute(sobely)

# 8비트로 변환하는 과정.
scaled_sobelx = np.uint8(255*abs_sobelx/np.max(abs_sobelx))
scaled_sobely = np.uint8(255*abs_sobely/np.max(abs_sobely))

# thresh 범위 내의 픽셀만 검출 (단위: 색상값(0~255))
thresh_min = 20
thresh_max = 100
sxbinary = np.zeros_like(scaled_sobelx)
sxbinary[(scaled_sobelx >= thresh_min) & (scaled_sobelx <= thresh_max)] = 1
sybinary = np.zeros_like(scaled_sobely)
sybinary[(scaled_sobely >= thresh_min) & (scaled_sobely <= thresh_max)] = 1

plt.imshow(sxbinary, cmap='gray')
#plt.imshow(sybinary, cmap='gray')
plt.show()

Input:

Output:
$sobel_x$의 결과
$sobel_y$의 결과

결과를 보면 $sobel_x$에서는 주로 수직선이, $sobel_y$에서는 주로 수평선이 검출되는 것을 볼 수 있습니다.
왜인진 모르겠지만 Sobel함수의 결과물을 cv2.imshow로 실행하면 이미지가 안보이고 plt.imshow 함수로 실행하면 이미지가 보입니다. 어떤 이유 때문인지 잘 모르겠네요.

Sobel Filter를 사용한 다양한 이미지 검출 방법

소벨 필터를 이용하여 이미지를 검출하는 방법은 총 4가지입니다. 둘은 앞서 설명한 $x$축 검출과 $y$축 검출입니다. $x$축 검출과 $y$축 검출을 그대로 사용하기도 하고 이 둘을 이용하여 검출된 다른 이미지를 사용하기도 합니다.

Magnitude of Gradient

$x$축, $y$축 검출 이외의 세 번째 차선 검출 방법은 그래디언트의 크기 검출입니다. 이 두 검출값을 조합하여 더 좋은 값을 찾는 과정입니다. 그 방식은 다음과 같습니다.

$\large{ abs\_sobelx = \sqrt{(sobel_x)^2} }$ $\large{ abs\_sobely = \sqrt{(sobel_y)^2} }$ $\large{ abs\_sobelxy = \sqrt{(sobel_x)^2+(sobel_y)^2} }$

$sobel_x$와 $sobel_y$의 제곱의 합의 제곱근입니다. 이 방식으로 $sobel_x$와 $sobel_y$의 값이 모두 반영된 값을 찾을 수 있습니다.

Magnitude of Gradient 예제

import cv2
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg

img = cv2.imread('/home/이미지 경로/sobel_ex.png')
gray = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
# Sobel(이미지, 이미지 비트 수, x축, y축)
sobelx = cv2.Sobel(gray, cv2.CV_64F, 1, 0)
sobely = cv2.Sobel(gray, cv2.CV_64F, 0, 1)

# Magnitude of Gradient
gradmag = np.sqrt(sobelx**2 + sobely**2)

# 8비트로 변환하는 과정.
scale_factor = np.max(gradmag) / 255
gradmag = (gradmag/scale_factor).astype(np.uint8)

# thresh 범위 내의 픽셀만 검출 (단위: Gradient, 단위없음)
thresh_min = 20
thresh_max = 100
binary = np.zeros_like(gradmag)
binary[(gradmag >= thresh_min) & (gradmag <= thresh_max)] = 1

plt.imshow(binary, cmap='gray')
plt.show()

Input:
Sobel Filter 예제의 입력값과 같습니다.

Output:

Direction of the Gradient

마지막으로, 그래디언트의 방향(각도)를 통해 차선을 검출할 수 있습니다. 차선은 항상 일직선이라고 가정했을 때, 자동차가 촬영하는 이미지의 수평선 즉 이미지의 $x$축과 이루는 각도가 일정합니다. 이 점을 이용하여 $sobel_x$와 $sobel_y$가 이루는 각도를 계산합니다.

$\large{ \theta = arctan(\frac{sobel_y}{sobel_x}) }$

Direction of the Gradient 예제

import cv2
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg

img = cv2.imread('/home/이미지 경로/sobel_ex.png')
gray = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)

# Sobel(이미지, 이미지 비트 수, x축, y축)
sobelx = cv2.Sobel(gray, cv2.CV_64F, 1, 0, ksize=15)
sobely = cv2.Sobel(gray, cv2.CV_64F, 0, 1, ksize=15)
# Gradient 방향의 절댓값 (0~pi/2)
absgraddir = np.arctan2(np.absolute(sobely),np.absolute(sobelx))

# thresh 범위 내의 픽셀만 검출 (단위: radian)
thresh_min = 0.7
thresh_max = 1.3
binary = np.zeros_like(absgraddir)
binary[(absgraddir >= thresh_min) & (absgraddir <= thresh_max)] = 1

plt.imshow(binary, cmap='gray')
plt.show()

Input:
Sobel Filter 예제의 입력값과 같습니다.

Output:

노이즈가 많지만 차선은 검출해 내고 있습니다.

Color Spaces

차선을 검출하는 다른 방법은 색공간을 이용하는 것입니다. 우리는 주로 Grayscale을 통해 채널 줄이기 & 흰색, 노란색 검출을 하였지만, 노란색 차선은 종종 Grayscale을 하면 사라져버리는 경우도 있습니다. 이 점을 보완하기 위해 우리는 다른 색공간을 이용합니다. 다음 그림은 이미지를 각각 RGB의 3채널로 분리한 것입니다.
검출 결과를 보면 R채널과 G채널은 노란색 차선을 잘 검출합니다. 하지만 노란색에 B(Blue)성분이 없기 때문에 B채널에서는 잘 검출이 안되는 모습을 볼 수 있습니다. 하지만 R, G채널도 너무 밝은 부분에서는 노란색 선이 잘 검출되지 않습니다. 이 점을 보완하기 위해 우리는 HSV/HLS 색공간에 대해서 알아보겠습니다.

HSV Color spaces

이번 강의에서는 HSV 색공간을 다루지 않습니다. 개념만 간단하게 설명하고 넘어가겠습니다.
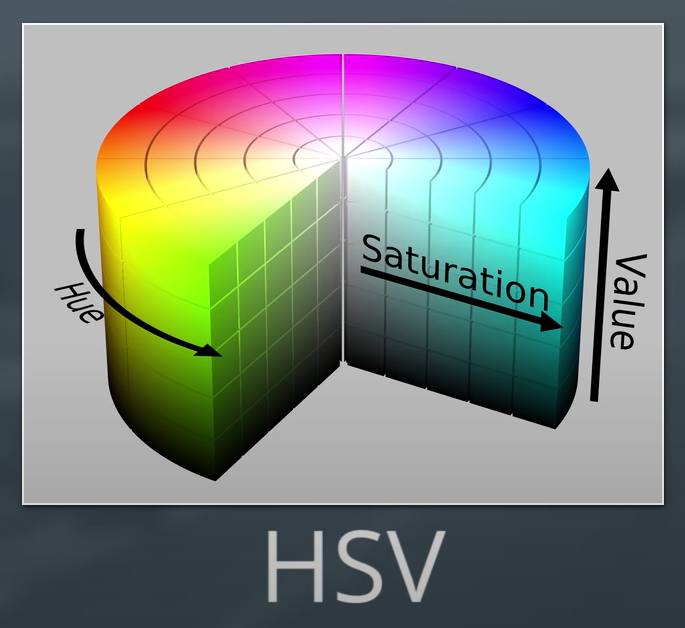
HSV 색공간에서의 H, S, V는 각각 다음과 같습니다.

• H(Hue): 색상, 원색을 나타냅니다. 한 색을 딱 정하고, $x$, $y$축을 S, V값으로 조정하는 방식입니다.
• S(Saturation): 채도, 가장 진한 상태를 100%로 나타내는 진함의 정도를 말합니다. 낮을수록 원색이 옅어집니다.
• V(Value): 명도, 색의 밝은 정도를 나타냅니다. 이 값이 낮을수록 검은색에, 높을수록 원색에 가깝습니다.

HLS Color spaces

이 게시글에서 다루는 색공간은 HLS 색공간입니다.

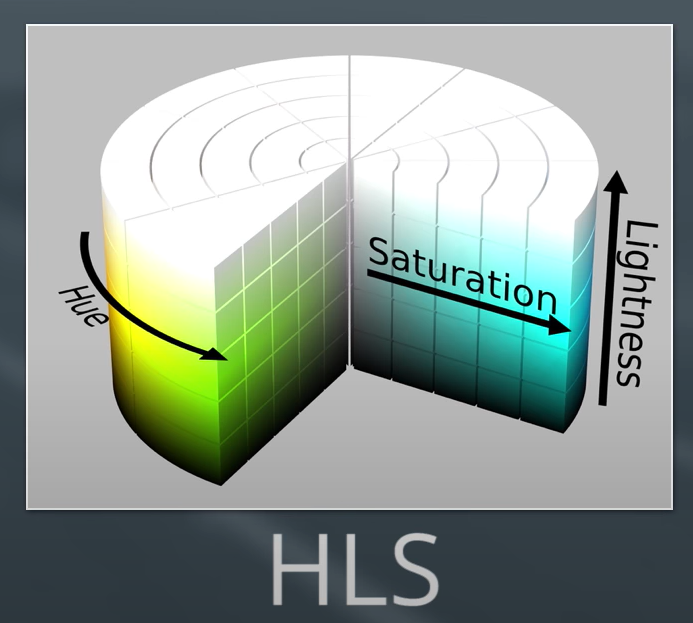
• H, S: HSV 색공간의 H, S와 동일합니다.
• L(Lightness): 밝기, 높은 값으로 갈수록 흰색에 가까운 색입니다.

이 색공간을 이용하여 채널을 분리해 봅시다.
분리 결과 S 채널의 이미지의 차선이 가장 선명하게 드러납니다. 이제 우리는 S 채널 이미지를 사용할 것입니다.

Color Threshold

검출한 이미지를 이진적으로 처리하는 과정입니다. 위의 과정들에서도 많이 했지만, S 채널의 threshold 결과물을 한번 보도록 하겠습니다.

차선이 훨씬 선명하게 검출되었습니다. threshold 값을 지정하는 구문은 다음과 같습니다. 예시는 S 채널 이미지입니다.

thresh = (90, 255)
binary = np.zeros_like(S)
binary[(S > thresh[0]) & (S <= thresh[1])] = 1

이와 같은 방식으로 차선을 검출합니다.

HLS Color spaces 예제

사실 단지 해당 채널을 검출하는 예제이므로 복잡하지는 않습니다.

import cv2
import numpy as np

img = cv2.imread('/home/이미지 경로/sobel_ex3.png')
hls = cv2.cvtColor(img, cv2.COLOR_RGB2HLS)

# H, L, S 채널 분리
H = hls[:, :, 0]
L = hls[:, :, 1]
S = hls[:, :, 2]

cv2.imshow('Result', S)
cv2.waitKey()

Input:

Output:

강의에서 본 결과와는 조금 다릅니다… 하지만 HLS 중에서 가장 괜찮은 결과입니다. 이제 threshold를 도입하여 binary 이미지를 만들어 보겠습니다.

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('/home/이미지 경로/sobel_ex3.png')
hls = cv2.cvtColor(img, cv2.COLOR_RGB2HLS)

# H, L, S 채널 분리
H = hls[:, :, 0]
L = hls[:, :, 1]
S = hls[:, :, 2]

# threshold 설정, binary 이미지 추출
thresh = (90, 255)
binary = np.zeros_like(S)
binary[(S > thresh[0]) & (S <= thresh[1])] = 1

plt.imshow(binary, cmap='gray')
plt.show()

Input:
HLS 채널 분리 예제와 같습니다.

Output:

HLS 채널 분리 예제의 결과는 조금 의아했지만, 결국 binary 처리를 하고 나니 좋은 결과가 나왔습니다.

Combine Color spaces and Gradient

마지막으로 색공간으로 검출한 이미지와 소벨 필터로 검출한 이미지를 합치는 과정입니다.
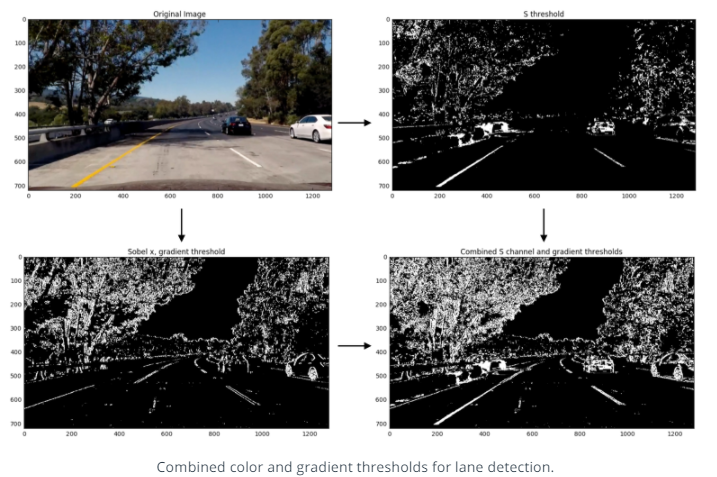
두 이미지는 다음 구문과 같은 방법으로 결합할 수 있습니다.

combined_binary = np.zeros_like(sxbinary)
combined_binary[(s_binary == 1) | (sxbinary == 1)] = 1

질문

1. 소벨 필터는 마스크+$\sum$하는 과정을 모두 합쳐서고, 소벨 마스크는 3$\times$3 행렬만을 말하는 건가요?
2. Direction of the Gradient를 통해 차선 검출 방법에서 커브를 트는 차선도 검출할 수 있나요?
3. $sobel_x$의 결과가 가장 좋다고 하던데, 다 똑같아보여서 잘 모르겠습니다…
4. 왜 소벨 필터의 결과는 plt.imshow함수로만 제대로 보이나요? cv2.imshow 함수는 검은색 화면만 보이는 이유
5. 8비트 변환은 왜 하나요? (그림은 8비트 변환을 안했을때의 결과)
6. Sobel 함수의 결과물은 그래디언트값, 그래디언트 방향은 어떤 각도를 말하는 건가요?
7. HLS 공간을 쓰는 이유는 무엇인가요? RGB는 잘 안보여서 그런거라 하던데 HSV는 안되나요? 굳이 HLS 색공간을 골라 쓰는 이유가 뭔가요?

참고 사이트

Udacity Self-driving car nanodegree - Gradient and Color Spaces(링크 공유 불가능)
Programming 블로그 - 1차 미분 마스크, 2차 미분 마스크

Refstop

Deep Learning 및 SLAM을 공부하고 있습니다.

Comments

  Write a comment ...