제대로 된 이미지로 보정하기

컴퓨터 비전에서 사용하는 센서 중 가장 중요한 것은 단연코 카메라입니다. 이미지 처리가 주된 내용인 만큼 카메라가 감지하는 정보는 높은 정확도를 요구합니다. 하지만 공장에서 만들어지기만 한 카메라를 바로 사용하기에는 문제가 있습니다. 내부 파라미터 조정이나 렌즈에 의한 왜곡 등이 아직 보정되지 않았기에 왜곡된 이미지가 출력될 수 있습니다. 이러한 상태의 카메라의 이미지를 보정하는 과정은 다음과 같습니다.

1. 카메라 캘리브레이션(Camera Calibration)
2. 왜곡 교정 (Distortion Correction)
3. 원근 변환 (Perspective Transform)

사실 원근 변환은 이미지를 보정하는 과정보다는 가공하는 과정에 가깝지만 이번 강의에서 소개해주는 김에 다루도록 하겠습니다.

카메라 캘리브레이션 (Camera Calibration)

카메라 캘리브레이션은 간단히 말하면 3차원의 형상을 2차원으로 온전히 옮길 수 있도록 도와주는 파라미터들을 도출하는 과정입니다. 카메라 영상은 3차원 형상을 2차원으로 옮길 때 3차원 공간상의 점들을 외부 파라미터(extrinsic parameter)와 내부 파라미터(intrinsic parameter)에 곱하여 나타냅니다. 다음의 공식은 3차원 월드 좌표계 $(X, Y, Z)$의 점을 2차원 평면 좌표계 $s(x, y)$로 변환하는 공식입니다.

$\large{ s \begin{bmatrix} x\\ y\\ 1 \end{bmatrix}=\begin{bmatrix} f_x & skew\_cf_x & c_x\\ 0 & f_y & c_y\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_1\\ r_{21} & r_{22} & r_{23} & t_2\\ r_{31} & r_{32} & r_{33} & t_3 \end{bmatrix} \begin{bmatrix} X\\ Y\\ Z\\ 1 \end{bmatrix}=A[R|t]\begin{bmatrix} X\\ Y\\ Z\\ 1 \end{bmatrix} }$

이 공식을 살펴보면 우선 월드 좌표계의 점 $(X, Y, Z)$를 회전 변환하여 카메라 좌표계에서의 점으로 변환시킵니다. 그 후 카메라 내부 파라미터를 곱하여 2차원의 점으로 변환합니다. 이때 변환된 좌표계를 이미지 좌표계라고 하며, 공식에서 $s(x, y, 1)$에 해당합니다. 좌표계들을 그림으로 표현하면 다음과 같습니다.

하지만 현재 우리가 공장에서 막 나온 카메라를 가지고 있다고 하면, 위의 공식에서 모르는 요소가 두 개 있습니다. 바로 외부 파라미터와 내부 파라미터입니다.

1. 외부 파라미터

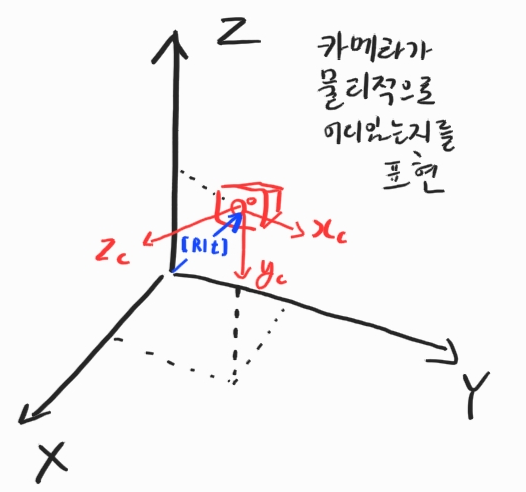
외부 파라미터는 월드 좌표계와 카메라 좌표계 사이의 관계입니다. 쉽게 말하면 물리적인 관계입니다. 카메라가 월드 좌표계로부터 얼마만큼 병진이동했는지($[R|t]$ 중 $t$, $\begin{bmatrix} t_1\ t_2\ t_3 \end{bmatrix}$), 얼마만큼 회전이동했는지($[R|t]$ 중 $R$, $\begin{bmatrix} r_{11} & r_{12} & r_{13} \ r_{21} & r_{22} & r_{23} \ r_{31} & r_{32} & r_{33} \end{bmatrix}$)를 나타냅니다. 사실 이 부분은 카메라 캘리브레이션의 결과값에 도출되는 부분은 아닙니다.

2. 내부 파라미터

내부 파라미터는 카메라 좌표계와 이미지 좌표계 사이의 관계입니다. 내부 파라미터의 구성요소는 크게 초점거리 $(f_x, f_y)$, 주점 $(c_x, c_y)$, 그리고 비대칭 계수 $skew_c$로 이루어져 있습니다. 간단히만 설명하겠습니다. 자세한 내용은 다음 블로그를 참고해 주시기 바랍니다.

핀홀 카메라

내부 파라미터의 구성요소를 설명하기에 앞서 내부 파라미터에 사용되는 이상적인 카메라 모델인 핀홀 카메라를 소개하겠습니다. 핀홀 카메라는 바늘구멍이라는 초점이 있는 카메라입니다. 이 게시글은 핀홀 카메라를 기준으로 설명됩니다.

1. 초점 거리(focal length) $(f_x, f_y)$

초점거리는 센서로부터 렌즈 중심까지의 거리를 의미합니다. 단위는 픽셀이며 이미지 센서의 셀의 크기에 종속된 값입니다. 만약 셀의 크기가 0.1mm이고 초점 거리가 500픽셀이라면, mm단위의 초점거리는 50mm입니다.

2. 주점(principle point) $(c_x, c_y)$

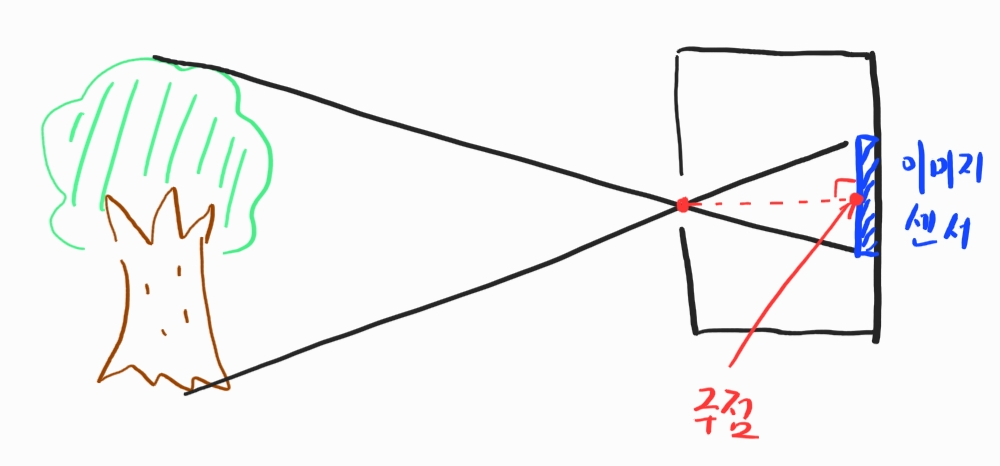
주점은 카메라 렌즈의 중심으로부터 이미지 센서에 내린 수선의 발을 말합니다. 단위는 픽셀로 역시 셀의 크기에 종속되어 있습니다. 영상 중심점과 같은 값을 보이기도 하지만 카메라 조립과정 중 오차로 렌즈와 이미지 센서의 수평이 어긋나면 다른 값이 나옵니다.

3. 비대칭 계수(skew coefficient) $skew_c$

비대칭 계수는 이미지 센서의 셀 array의 y축이 기울어진 정도를 나타냅니다. 표현은 $skew_c=tan(\alpha)$로 나타냅니다. 요즘 카메라들은 skew 에러가 거의 없기 때문에 비대칭 계수는 잘 고려하지 않는다고 합니다.

결과적으로 이렇게 사용

그림은 카메라 좌표계의 $Z_C$축을 가로축으로 나타내어 사용법을 설명합니다. 카메라 좌표계 위의 한 점 $(X_C, Y_C, Z_C)$을 가지고 이미지 좌표계 위에 나타내는 방법을 보겠습니다.
초점으로부터 광학축 $Z_C$를 따라 거리가 1인 평면을 정규 이미지 평면(Normalized Image Plane)이라고 합니다. 이것은 이미지 평면을 정규화시킨 것으로 실제로 존재하는 평면은 아닙니다. 카메라 좌표계의 점을 정규 이미지 평면으로 투영(projection)시켜 정규 이미지 평면상의 좌표로 변환합니다. 이 평면은 $Z_C=1$이란 특징을 갖고 있으므로 $(X_C, Y_C, Z_C)$를 $Z_C$로 나누어 $Z_C$ 좌표를 1로 만들어 줍니다. 따라서 점 $(X_C, Y_C, Z_C)$를 정규 이미지 평면에 나타낸 점은 $(\frac{X_C}{Z_C},\frac{Y_C}{Z_C},1)$입니다. 그림에서의 $(u, v)$에 해당하는 점입니다.
이제 다시 이 점을 이미지 평면으로 올려 줍시다. 이미지 평면의 특징은 $Z_C=f$라는 것입니다. 따라서 정규화되었던 $Z_C$에 초점거리 $f$만 곱해 준다면 이미지 평면에 점을 올려줄 수 있습니다. 위의 공식에서 $s$란 바로 초점거리 $f$를 말하는 것입니다. 따라서 $Z_C=f$일 때 이미지 평면상의 점 좌표는 $(f_x\frac{X_C}{Z_C}, f_y\frac{Y_C}{Z_C}, f)$입니다. 이미지 평면상의 좌표기는 하지만 아직 그림에서의 $(x,y)$ 점은 아닙니다.
마지막으로 이미지에서 픽셀좌표는 이미지의 중심이 아닌 좌상단 모서리를 원점으로 하기 때문에 렌즈 중심에서 셀에 내린 수선의 발인 주점을 좌표에 더하여 줍니다. 따라서 최종적인 좌표는 $(f_x\frac{X_C}{Z_C}+C_x, f_y\frac{Y_C}{Z_C}+C_y, f)$이 됩니다. 물론 이 좌표는 카메라 좌표계적 표현이고, 이미지 평면의 점은 $(f_x\frac{X_C}{Z_C}+C_x, f_y\frac{Y_C}{Z_C}+C_y)$입니다. 그림에서의 $(x,y)$에 해당하는 점입니다. 식을 정리하면 다음과 같습니다.

$\large{ 1.\;\;(X_C, Y_C, Z_C)\;\;\xrightarrow[정규화]{}\;\;(\frac{X_C}{Z_C},\frac{Y_C}{Z_C},1)\;\;\;\;\;\;(u,v)=(\frac{X_C}{Z_C},\frac{Y_C}{Z_C}) }$ $\large{ 2.\;\;(\frac{X_C}{Z_C},\frac{Y_C}{Z_C},1)\;\;\xrightarrow[이미지\;평면화]{}\;\;(f\frac{X_C}{Z_C},f\frac{Y_C}{Z_C},f)\;\;\;\;\;\;(x',y')=(f\frac{X_C}{Z_C},f\frac{Y_C}{Z_C}) }$ $\large{ 3.\;\;(f\frac{X_C}{Z_C},f\frac{Y_C}{Z_C},f)\;\;\xrightarrow[원점을\;주점으로]{}\;\;(f\frac{X_C}{Z_C}+C_x,f\frac{Y_C}{Z_C}+C_y,f) }$ $\large{ (x,y)=(f\frac{X_C}{Z_C}+C_x,f\frac{Y_C}{Z_C}+C_y) }$

정규화의 의미

규칙이 없는 데이터에서 어떤 조건을 부여함로서 규칙을 따르는 데이터로 만드는 것을 의미합니다.

카메라 캘리브레이션 예제

왜곡 교정 (Distortion Correction)

이미지 보정의 다음 과정은 왜곡 교정입니다. 왜곡이란 카메라가 완벽한 이미지를 생성하지 못해 이미지가 휘어져 보이는 것인데, 차선 인식을 목표로 하는 우리에겐 치명적인 결함입니다. 따라서 이미지의 일부, 특히 가장자리 근처에 있는 요소가 늘어나거나 기울어질 수 있어 이를 수정해 주어야 합니다. 이미지 왜곡 해제는 차선 인식 뿐만 아니라 다른 이미지 처리에서도 가장 기본적인 단계입니다.
왜곡의 종류에는 두 가지가 있습니다.

1. 방사 왜곡 (Radial Distortion)
2. 접선 왜곡 (Tangential Distortion)

1. 방사 왜곡 (Radial Distortion)

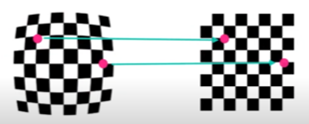
방사 왜곡은 볼록렌즈의 굴절률에 의한 것으로 그림과 같이 왜곡 정도가 중심에서 이미지의 가장자리로 갈수록 왜곡이 심해지는 형태입니다.
방사 왜곡의 수학적 모델은 다음과 같습니다.

$\large{ x_{corrected}=x(1+k_1r^2+k_2r^4+k_3r^6) }$ $\large{ y_{corrected}=y(1+k_1r^2+k_2r^4+k_3r^6) }$

2. 접선 왜곡 (Tangential Distortion)

접선 왜곡은 카메라 제조 과정에서 렌즈와 이미지 센서의 수평이 맞지 않거나 렌즈 자체의 centering이 맞지 않아서 발생합니다.
접선 왜곡의 수학적 모델은 다음과 같습니다.

$\large{ x_{corrected}=x+[2p_1xy+p_2(r^2+2x^2)] }$ $\large{ y_{corrected}=y+[p_1(r^2+2y^2)+2p_2xy] }$

따라서 왜곡 교정을 위해서는 총 5개의 파라미터가 필요합니다. 이 파라미터를 왜곡 계수라고 합니다.

$\large{ Distortion coefficient = (k_1\;k_2\;p_1\;p_2\;k_3) }$

이 왜곡 계수는 카메라 캘리브레이션의 결과물로 도출됩니다.

왜곡이 반영된 수학적 모델

렌즈계 왜곡이 없다고 할 때, 3차원 공간상의 한 점을 정규 이미지 평면에 나타내면 다음과 같습니다.
(첨자 $n: normalized, u:undistorted$)

$\large{ \begin{bmatrix} x_{n\_u} \\ y_{n\_u} \end{bmatrix}=\begin{bmatrix} \frac{X_C}{Z_C} \\ \frac{Y_C}{Z_C} \end{bmatrix} }$

하지만 실제로 카메라로 찍은 영상은 왜곡이 발생합니다. 왜곡의 수학적 모델을 반영된 모델은 다음과 같습니다.
(첨자 $d:distorted$)

$\large{ \begin{bmatrix} x_{n\_d} \\ y_{n\_d} \end{bmatrix}=(1+k_1r^2+k_2r^4+k_3r^6)\begin{bmatrix} x_{n\_u} \\ y_{n\_u} \end{bmatrix}+\begin{bmatrix} 2p_1xy+p_2(r^2+2x^2) \\ p_1(r^2+2y^2)+2p_2xy \end{bmatrix} }$

단,

$\large{ r_u^2=x_{n\_u}^2+y_{n\_u}^2 }$

위 수식에서 우변의 첫번째 항은 방사 왜곡, 두번째 항은 접선 왜곡을 나타냅니다. 이 공식에서 방사 왜곡과 접선 왜곡의 수학적 모델은 왜곡을 보정하는 것이 아닌 왜곡을 반영하는 모델이라는 것을 알 수 있습니다. $r_u$는 왜곡이 없을 때의 중심, 즉 주점까지의 거리(반지름)입니다. 결국, 왜곡된 영상의 실제 영상 좌표 $(x_{p_u}, y_{p_u})$는 카메라 내부 파라미터를 반영하여 다음과 같이 구해집니다.

$\large{ \begin{bmatrix} x_{p\_d} \\ y_{p\_d} \\ 1 \end{bmatrix}=\begin{bmatrix} f_x & skew\_cf_x & c_x\\ 0 & f_y & c_y\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x_{n\_d} \\ y_{n\_d} \\ 1 \end{bmatrix} }$

즉,

$\large{ x_{p\_d}=f_x(x_{n\_d}+skew\_cy_{n\_d})+c_x }$ $\large{ y_{p\_d}=f_yy_{n\_d}+c_y }$

왜곡의 교정 단계

위의 단계에서 왜곡된 이미지의 모델을 살펴보았습니다. 이제 왜곡된 이미지로부터 교정된 이미지를 구하는 법을 살펴보겠습니다. 전체적인 방법은 교정 영상에서의 이미지를 역순의 변환을 통해 픽셀 좌표값을 왜곡된 이미지에 대응되는 픽셀 좌표에 채우는 것입니다. 다음 그림과 같습니다.
왜곡되지 않은 이미지의 모델 역시 위의 공식을 따릅니다. 왜곡되지 않은 경우 공식은 다음과 같습니다.

$\large{ \begin{bmatrix} x_{p\_u} \\ y_{p\_u} \\ 1 \end{bmatrix}=\begin{bmatrix} f_x & skew\_cf_x & c_x\\ 0 & f_y & c_y\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x_{n\_u} \\ y_{n\_u} \\ 1 \end{bmatrix} }$

우리가 *이미 교정된 이미지 $\begin{bmatrix} x_{p_u}
y_{p_u}
1 \end{bmatrix}$를 알고 있다고 할 때, 이 공식에 역행렬을 취하여 정규 이미지 평면의 좌표 $\begin{bmatrix} x_{n_u}
y_{n_u}
1 \end{bmatrix}$로 변환합니다.

$\large{ \begin{bmatrix} x_{n\_u} \\ y_{n\_u} \\ 1 \end{bmatrix}=\begin{bmatrix} f_x & skew\_cf_x & c_x\\ 0 & f_y & c_y\\ 0 & 0 & 1 \end{bmatrix}^{-1}\begin{bmatrix} x_{p\_u} \\ y_{p\_u} \\ 1 \end{bmatrix} }$

즉,

$\large{ x_{n\_d}=\frac{x_{p_u}-c_x}{f_x}-skew\_cy_{n\_u} }$ $\large{ y_{n\_d}=\frac{y_{p_u}-c_y}{f_y} }$

그 다음, $r_u^2=x_{n_u}^2+y_{n_u}^2$ 공식으로 $r_u$를 구하고 왜곡 모델을 적용하여 왜곡된 좌표 $(x_{n_d}, y_{n_d})$를 구합니다.

$\large{ \begin{bmatrix} x_{n\_d} \\ y_{n\_d} \end{bmatrix}=(1+k_1r^2+k_2r^4+k_3r^6)\begin{bmatrix} x_{n\_u} \\ y_{n\_u} \end{bmatrix}+\begin{bmatrix} 2p_1xy+p_2(r^2+2x^2) \\ p_1(r^2+2y^2)+2p_2xy \end{bmatrix} }$

마지막으로 $(x_{n_d}, y_{n_d})$를 다시 픽셀 좌표계로 변환하면 $(x_{n_u}, y_{n_u})$의 왜곡된 영상에서의 좌표 $(x_{p_d}, y_{p_d})$를 구할 수 있습니다.

$\large{ \begin{bmatrix} x_{p\_d} \\ y_{p\_d} \\ 1 \end{bmatrix}=\begin{bmatrix} f_x & skew\_cf_x & c_x\\ 0 & f_y & c_y\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x_{n\_d} \\ y_{n\_d} \\ 1 \end{bmatrix} }$

왜곡 교정 예제

OpenCV에서는 사용자가 이런 복잡한 과정을 거칠 필요 없이 undistort라는 왜곡 교정 함수가 존재합니다. 이 함수의 파라미터에 대해서 살펴보겠습니다.

cv2.undistort(img, mtx, dist, None, mtx)

• img: 왜곡이 있는 이미지
• mtx: 카메라 내부 파라미터
• dist: 왜곡 계수 위의 이론에서 사용한 요소들을 함수의 파라미터에 input합니다.

저는 예제를 이용했기 때문에 카메라 캘리브레이션의 결과값이 담긴 pickle 파일을 사용하여 불러왔습니다.

import pickle
import cv2
import numpy as np

dist_pickle = pickle.load( open( "/home/pickle 파일 경로/wide_dist_pickle.p", "rb" ) )
mtx = dist_pickle["mtx"]
dist = dist_pickle["dist"]

img = cv2.imread('/home/이미지 파일 경로/test_image2.png')
nx = 8 
ny = 6 

# 왜곡 보정 함수 실행
undist = cv2.undistort(img, mtx, dist, None, mtx)
cv2.imshow('undist', undist)
cv2.waitKey()

Input:

Output:

왜곡이 잘 보정된 것을 볼 수 있습니다.

원근 변환 (Perspective Transform)

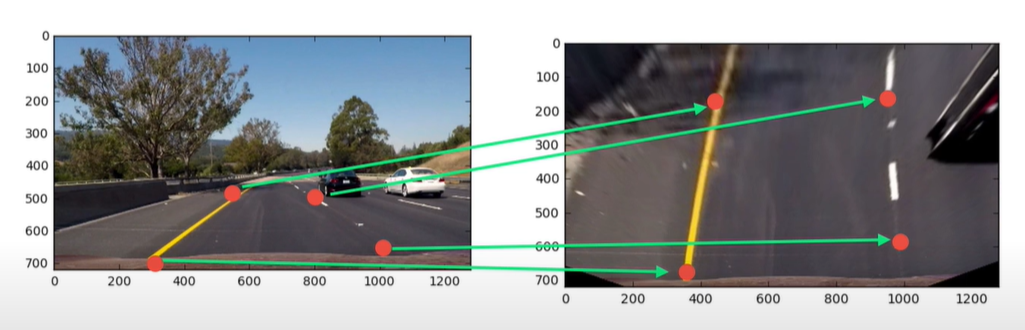
다른 각도나 방향에서 효과적으로 물체를 볼 수 있도록 이미지를 변형하는 기법입니다. 차선 인식에서 좌회전/우회전 시 방향을 틀 곳을 알아야 합니다. 컴퓨터 비전을 공부하는 우리가 알아야 할 것은 차선이 휘는 정도, 즉 차선의 곡률입니다. 하지만 우리는 카메라가 찍은 사진만으로는 차선이 휘었는지 직선인지 구분하기 어렵습니다. 다음 그림을 보면, 왼쪽 차선은 곡률이 있지만, 오른쪽 차선은 직선처럼 보입니다. 하지만 원근 변환을 통해 위에서 내려다 본 각도로 변환시키면, 곡률이 확실하게 드러납니다. 게다가 위에서 내려다보면 내 차의 현재 위치를 지도와 바로 매치시킬 수 있기 때문에 더 유용합니다. 이렇게 위에서 내려다본 형태로 사진을 가공하는 것을 조감도(Bird’s Eye View)라고 합니다.

이 조감도 모델을 만드는 원리는 네 점을 지정한 후, 그 점을 변환하여 위에서 내려다본 이미지를 생성하는 것입니다. 이러한 과정은 OpenCV의 getPerspectiveTransform 함수 내부에서 일어납니다.

차선의 곡률을 계산하는 방법 중 하나는 차선에 2차 다항식을 맞추는 것입니다. 그림과 같은 방법으로 말입니다.
하지만 이번 강의에서는 곡률은 구하지 않습니다. 다음 강의에서 구해보도록 합시다.

원근 변환 예제

OpenCV에서는 getPerspectiveTransform 함수를 통해 원근 변환 행렬을 구합니다.

import pickle
import cv2
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg

dist_pickle = pickle.load( open( "/home/pickle 파일 경로/wide_dist_pickle.p", "rb" ) )
mtx = dist_pickle["mtx"]
dist = dist_pickle["dist"]

img = cv2.imread('/home/이미지 파일 경로/test_image2.png')
nx = 8 # the number of inside corners in x
ny = 6 # the number of inside corners in y

def corners_unwarp(img, nx, ny, mtx, dist):
    undist = cv2.undistort(img, mtx, dist, None, mtx)
    gray = cv2.cvtColor(undist, cv2.COLOR_BGR2GRAY)
    ret, corners = cv2.findChessboardCorners(gray, (nx, ny), None)
    
    if ret == True:
        cv2.drawChessboardCorners(undist, (nx, ny), corners, ret)
        # corner 검출 결과를 더 잘 보기 위한 offset 설정, 상하좌우 100씩 여유를 줌.
        offset = 100 # offset for dst points
        # Grab the image shape
        img_size = (gray.shape[1], gray.shape[0])

        # src = 체스보드에서 검출된 corners의 네 끝점
        src = np.float32([corners[0], corners[nx-1], corners[-1], corners[-nx]])
        # destination point 목표 지점의 배열.
        dst = np.float32([[offset, offset], [img_size[0]-offset, offset], 
                                     [img_size[0]-offset, img_size[1]-offset], 
                                     [offset, img_size[1]-offset]])
        # 원근 변환 행렬 도출
        M = cv2.getPerspectiveTransform(src, dst)
        # 변환 행렬에 따라 이미지를 변환
        warped = cv2.warpPerspective(undist, M, img_size)
    return warped

top_down = corners_unwarp(img, nx, ny, mtx, dist)
cv2.imshow('Undistorted and Warped Image', top_down)
cv2.waitKey()

Input:
왜곡 교정 예제의 입력과 같습니다.

Output:

질문

Q1. 내부 파라미터의 구성요소가 무엇인진 알겠는데, 어떻게 구하는지를 모르겠습니다.
Q2. 비대칭 계수는 왜 이미지 좌표계 변환의 x에밖에 없나요?
Q3. 셀의 크기는 셀의 가로인가요 세로인가요?
A3. 초점거리의 $x$축, $y$축 성분에 따라 각각 가로 크기, 세로 크기로 계산합니다.
Q4. 실제 렌즈에서 초점이란?
Q5. 접선왜곡을 일부러 발생시키는 경우도 있다고 하는데 어디쓸려고 하는건가요?
A5. 왜곡을 일부러 Q6. *교정된 이미지를 만들려고 왜곡된 이미지와 픽셀 좌표를 대응시키는 것인데 이미 교정된 이미지가 있다면 그럴 필요가 있을까요?
왜곡된 이미지에서 교정된 이미지니까 반대 아닌가?

참고 사이트

Udacity Self-driving car nanodegree - Camera Calibration(링크 공유 불가능)
다크 프로그래머 블로그 - 카메라 캘리브레이션 (Camera Calibration)
다크 프로그래머 블로그 - 카메라 왜곡보정 - 이론 및 실제

Refstop

Deep Learning 및 SLAM을 공부하고 있습니다.

Comments

  Write a comment ...