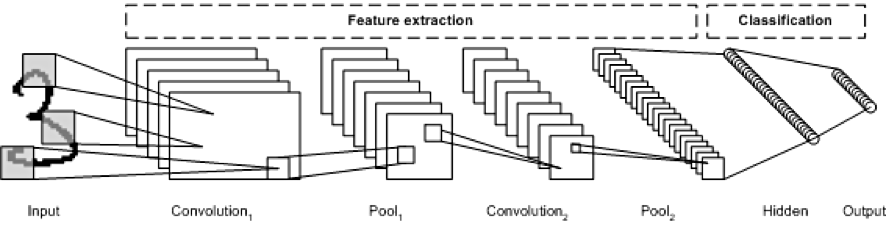
지금까지 우리는 심층 신경망(Deep Nerual Network)을 구성하기까지의 과정을 살펴보았습니다. 이제 이 심층 신경망으로 구성할 수 있는 네트워크 중 이미지 학습에 최적화된 합성곱 신경망(Convolutional Nerual Network, CNN)에 대해서 알아보겠습니다.
CNN이 되기까지
CNN이 고안되기 전에는 이미지를 Fully Connected Nerual Network라는 1차원 벡터 형태의 데이터를 학습하는 형태의 신경망 구조를 사용했습니다. 하지만 FNN은 몇 가지 단점이 있습니다.
첫번째로 이미지 데이터를 평면화 시키는 과정에서 이미지의 인접한 픽셀 간의 정보가 유실된다는 점입니다. FNN은 1차원 벡터 형태의 데이터를 입력받기 때문에 이미지의 인접 픽셀간의 상관관계를 반영할 수 없습니다. 반면 CNN은 이미지의 특징을 보존한 채로 학습을 진행하기 때문에 인접 픽셀간의 정보 유식을 막을 수 있습니다.
두번째 FNN의 문제점은 막대한 양의 model parameter입니다. 만약 FNN을 사용하여 (1024,1024)크기의 컬러 이미지를 처리하고자 한다면 FNN에 입력되는 벡터의 차원은 1024$\times$1024$\times$3=315만 개입니다. 약 300만 차원의 데이터를 처리하기 위해서는 막대한 양의 뉴런이 필요하고 이에 따라 model parameter의 개수는 더욱 많은 양이 필요할 것입니다. 하지만 CNN의 경우 필터들을
1. CNN의 주요 용어 정리
CNN에는 다음과 같은 용어들이 사용됩니다.
- Convolution(합성곱)
- 채널(Channel)
- 필터(Filter)
- 커널(Kernel)
- 스트라이드(Stride)
- 패딩(Padding)
- 피처 맵(Feature Map)
- 액티베이션 맵(Activation Map)
- 풀링(Pooling) 레이어
각 용어에 대해서 간략하게 정리하겠습니다.
1.1 Convolution Layer(합성곱)
Convolution은 합성곱이라는 의미인데, input 함수(신호)와 임펄스 응답 함수(신호)를 반전 이동한 값을 곱하여 적분한 값입니다. 원래의 의미는 이렇지만, 이해하기 너무 어려우므로 다음 gif 파일을 통해 쉽게 알 수 있습니다.
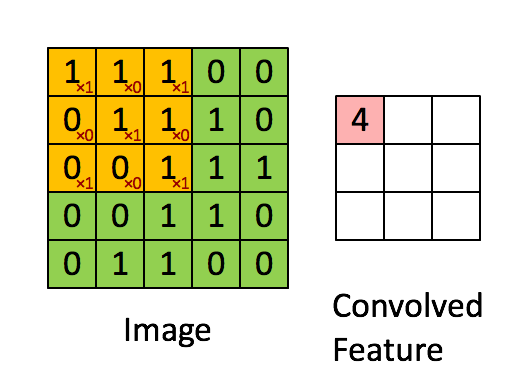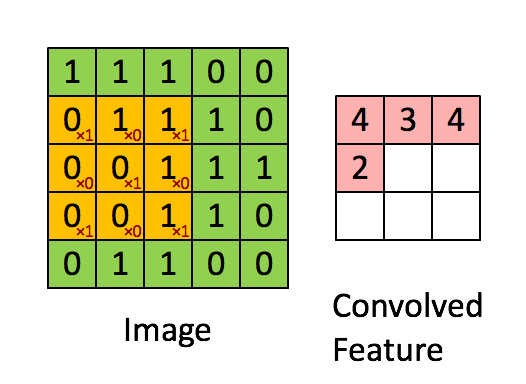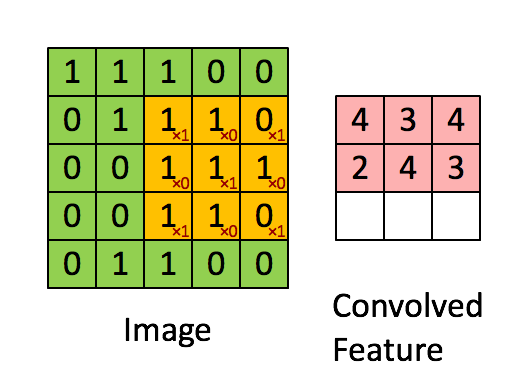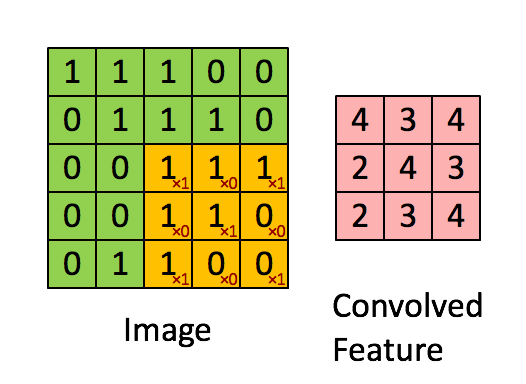
위의 gif 파일은 입력된 이미지 데이터를 필터를 통해 Feature Map을 만드는 과정입니다. 필터로 이미지를 훑어가면서 각각의 합성곱 결과를 저장하여 Feature Map을 구성합니다. CNN의 첫번째 과정인 Convolution Layer는 바로 이 Feature Map을 생성하는 과정입니다. Feature Map을 생성한 후 활성화 함수(Activation Function)에 통과시킨 출력을 액티베이션 맵(Activation Map)이라고 합니다.
1.2 채널(Channel)
채널은 이미지를 구성하고 있는 실수값의 차원입니다. 이미지를 색 공간에 따라서 분리할 때, RGB의 3채널로 분리할 수 있습니다. 이미지를 구성하는 각 픽셀은 실수로 표현한 3차원 데이터입니다. 각각의 차원은 R, G, B의 3색을 나타내는 실수로, 이때의 RGB를 채널이라고 합니다.

Convolution Layer에 입력되는 데이터는 필터가 적용되고, 하나의 필터당 하나의 Feature Map이 생성됩니다. 따라서 Convolution Layer에 n개의 필터가 적용된다면 출력되는 Feature Map은 n개의 채널을 갖게 됩니다.
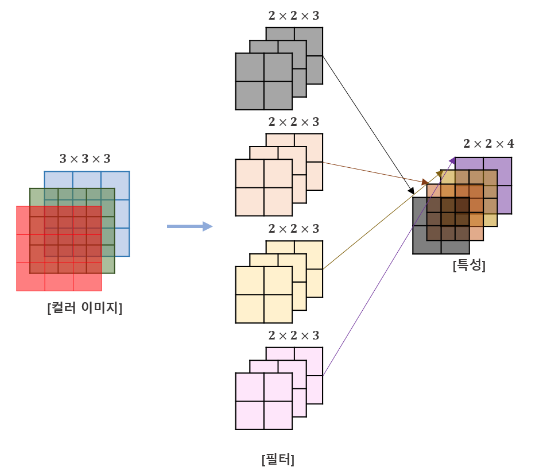
하지만 이번 게시글에서는 필터의 개수가 1개뿐인 모델만 다룰 것입니다.
1.3 필터(Filter), 커널(Kernel) & 스트라이드(Stride)
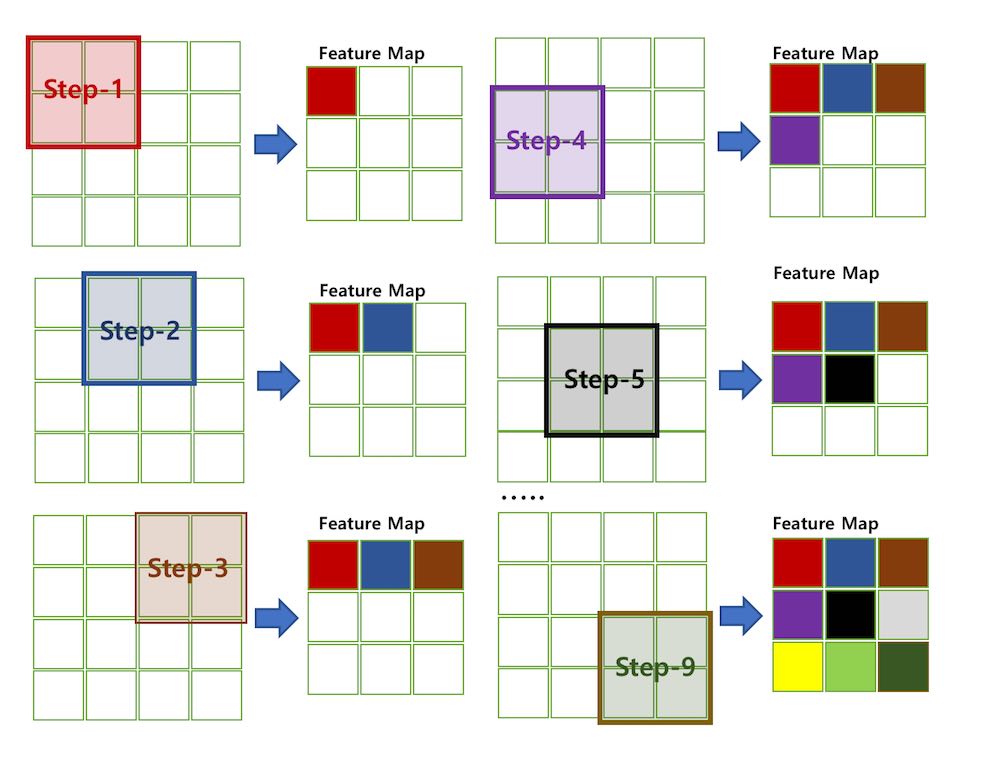
필터는 이미지의 특징을 찾아내기 위한 공용 파라미터입니다. 일반적으로 (4,4), (3,3)같은 정방행렬로 표현되고 사용 방법은 1.1의 gif 이미지에 잘 표현되어 있습니다. 필터는 이미지를 순회하면서 합성곱을 계산하여 Feature Map을 생성합니다. 이때 필터가 한번에 이동하는 간격을 Stride라고 합니다. Stride는 직역하면 보폭이라는 뜻으로 말 그대로 “필터가 한 걸음에 얼마나 가냐”를 의미하는 값입니다. 위의 gif 이미지의 Stride는 1입니다. 아래 이미지는 Stride가 1이고, 이미지 픽셀이 (16,16), 필터 크기가 (2,2)일때의 Feature Map 생성 과정을 나타낸 사진입니다.
입력 데이터가 여러 채널을 갖는 경우, 각 채널의 Feature Map을 모두 더한 값이 최종 출력이 됩니다. 따라서 입력 데이터의 채널 수와는 상관없이 필터의 개수에 따라 결정된다는 것을 알 수 있습니다.
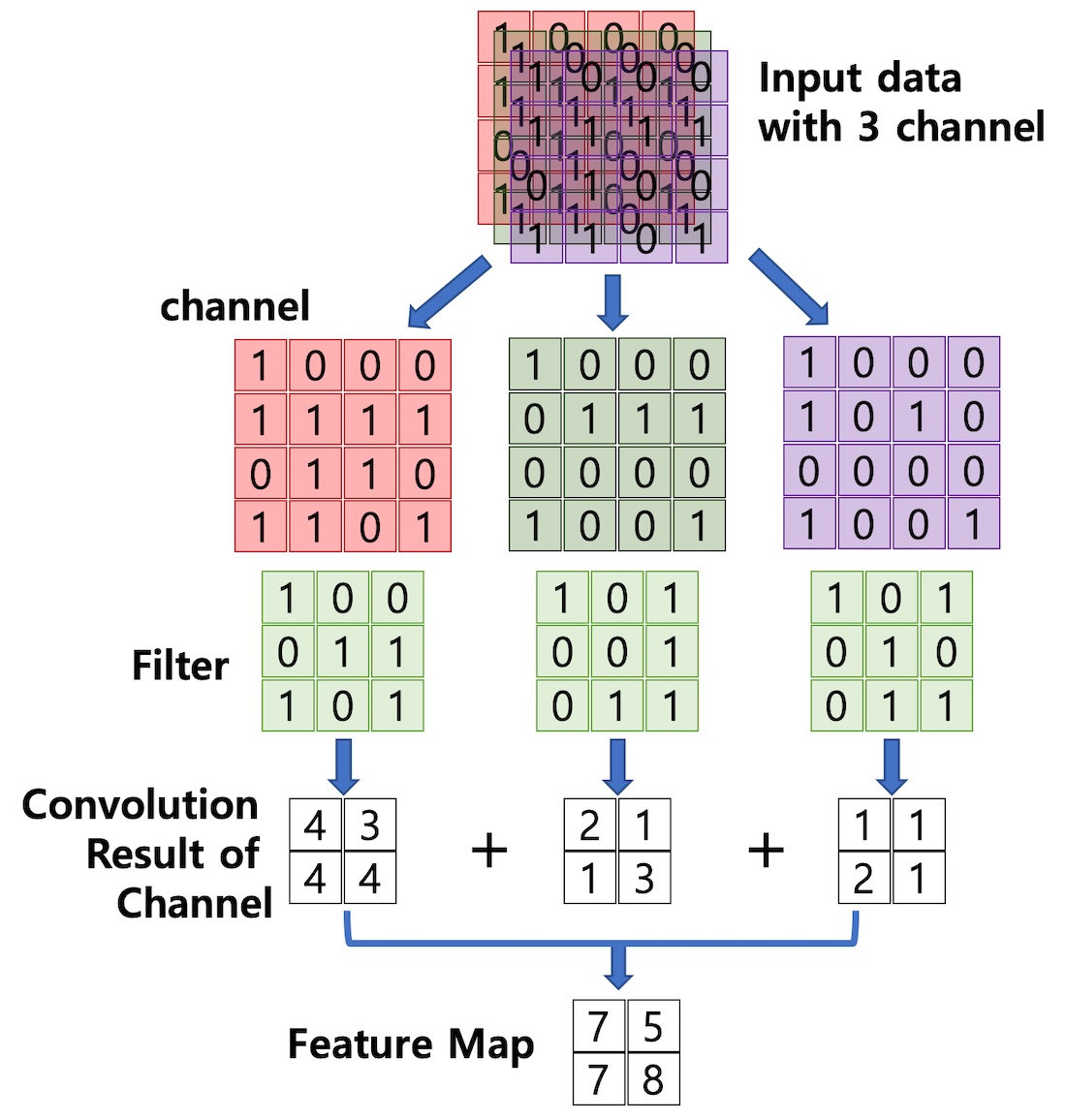
1.4 패딩(padding)
패딩은 Convolution layer에서 필터와 Stride의 작용으로 출력 Feature Map의 크기가 줄어드는 현상을 방지하고 출력 데이터의 사이즈를 조정하는 방법입니다. 단어 그대로 입력데이터에 패드를 부착하는 것처럼 이미지 외곽에 지정된 픽셀만큼 특정 값으로 채워넣습니다. 보통 CNN에서는 패딩값을 0으로 채웁니다.
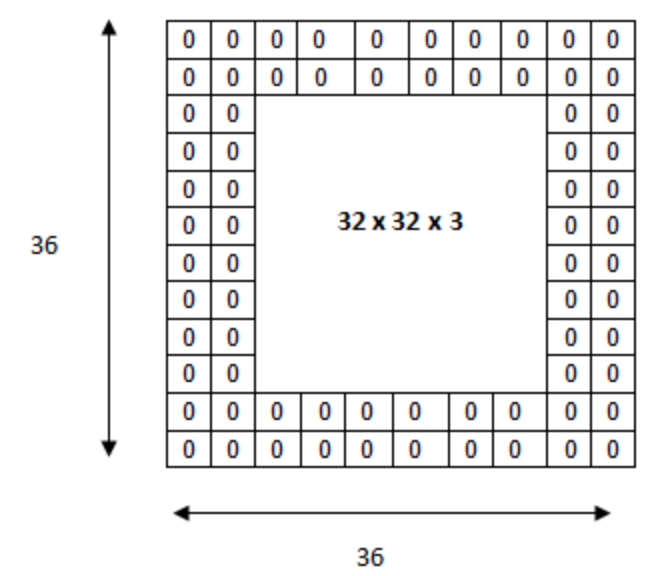
위의 이미지는 원래 입력 데이터 32$\times$32$\times$3 이미지에 2픽셀만큼의 패딩을 추가하여 36$\times$36$\times$3 이미지로 만든 것입니다. 출력 데이터의 사이즈를 조절하는 기능 이외에도 Convolution layer가 이미지의 외곽을 인식하는 학습 효과도 있습니다.
1.5 Pooling Layer
Pooling layer는 Convolution layer의 출력인 Activation Map을 입력으로 받아서 크기를 줄이거나 특정 데이터를 강조하는 용도로 사용됩니다. Pooling 처리 과정은 지정된 정방행렬 범위 내의 데이터를 Pooling 방식에 따라서 처리합니다. Pooling layer를 처리하는 방법으로는 Max pooling, Min pooling, Average pooling이 있습니다. 이름만 봐도 알 수 있듯이 각각 최댓값, 최솟값, 평균값만을 남기거나 계산하는 방식입니다. 다음 이미지를 참고하면 이해하기 쉽습니다.
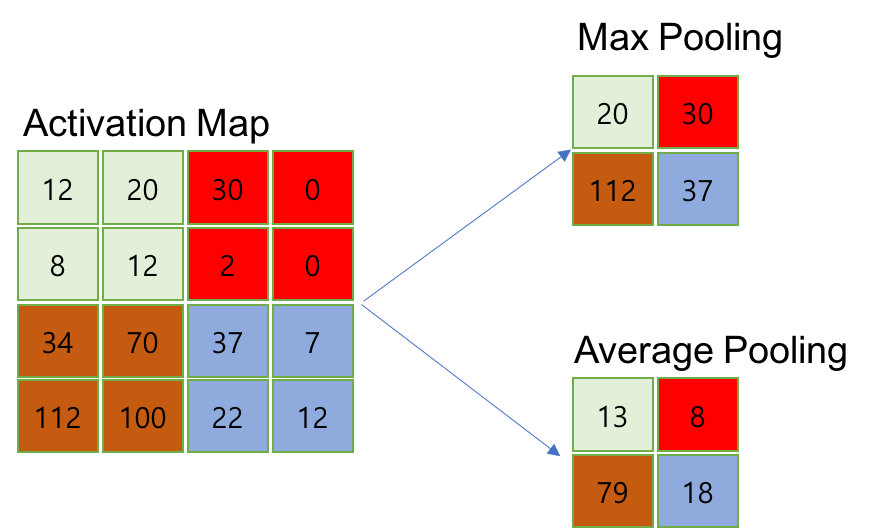
Pooling layer의 처리과정은 Convolution layer와 거의 비슷하지만 조금의 차이점이 있습니다.
- 학습대상 파라미터가 없음
- 행렬의 사이즈 감소
- 채널 수 변경 없음
CNN에서는 주로 Max pooling을 사용합니다.
2. 레이어별 출력 데이터 계산
Convolution layer와 Pooling layer의 출력 데이터 크기를 계산하는 방법을 정리했습니다.
2.1 Convolution layer 출력 데이터 크기 계산
입력 데이터에 대한 필터의 크기와 Stride 크기에 따라서 Feature Map 크기가 결정됩니다.
- 입력 데이터 높이: H
- 입력 데이터 폭: W
- 필터 높이: FH
- 필터 폭: FW
- Stride 크기: S
- Padding 사이즈: P
$Output\;Height=OH=\frac{(H+2P-FH)}{S}+1$
$Output\;Width=OW=\frac{(W+2P-FW)}{S}+1$
위 식의 결과는 자연수가 되어야 합니다. 또한 Convolution layer 다음에 Pooling layer가 온다면, Feature Map의 행과 열 크기는 Pooling 크기의 배수여야 합니다. 만약 Pooling 사이즈가 (3,3)이라면 위 식의 결과는 자연수이고 3의 배수여야 합니다. 이 조건을 만족하도록 Filter의 크기, Stride의 간격, Pooling 크기 및 패딩 크기를 조절해야 합니다.
2.2 Pooling layer 출력 데이터 크기 계산
Pooling layer의 Pooling 사이즈는 일반적으로 정방행렬입니다. 또한 Convolution layer의 출력이 Pooling 사이즈의 정수배가 되도록 하여 Pooling layer의 출력 사이즈를 결정하게 됩니다. 예를 들어 Convolution layer의 출력 Activation Map 사이즈가 (6,6)이고 Pooling 사이즈가 (3,3)이면, Pooling layer의 출력 사이즈는 (2,2)가 됩니다. 따라서 Pooling layer의 출력 사이즈는 다음과 같이 계산할 수 있습니다.
$Output\;Row\;Size=\frac{Input\;Row\;Size}{Pooling\;Size}$
$Output\;Column\;Size=\frac{Input\;Column\;Size}{Pooling\;Size}$
마무리
이번 게시글에서는 CNN에서 사용되는 용어 및 입출력 데이터의 크기를 계산하는 방법을 알아보았습니다. 다음 게시글은 이 게시글에 이어 LeNet-5 네트워크 구성과 직접적인 예시를 들어 파라미터를 계산해 보도록 하겠습니다.
참고 사이트
TAEWAN.KIM 블로그 - “CNN, Convolutional Neural Network 요약”
Untitled 블로그 - “[머신 러닝/딥 러닝] 합성곱 신경망 (Convolutional Neural Network, CNN)과 학습 알고리즘”
YJJo 블로그 - “Convolution Nerual Networks (합성곱 신경망)”
Refstop
Deep Learning 및 SLAM을 공부하고 있습니다.










Comments