쿼터니안이란?
오일러 공식에 의해 복소수를 삼각함수로 표현할 수 있다는 점에 착안하여 삼각함수 없이도 회전변환 할 수 있게 해주는 방법. (수정)
오일러 공식을 허수 평면에서 나타내면 다음과 같다.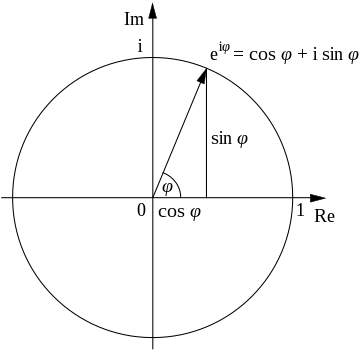
즉, 오일러 공식을 통해 좌표 $(x, y)$를 각도 $\theta$만큼 회전시킬 수 있는 것이다.
실제로 $e^{i \theta} \cdot (x+iy)$를 하면 2차원 유클리디언 공간에서 각도 $\theta$만큼 회전한 좌표가 나온다.
오일러 공식에 의해 복소수를 삼각함수로 표현할 수 있다는 점에 착안하여 삼각함수 없이도 회전변환 할 수 있게 해주는 방법. (수정)
오일러 공식을 허수 평면에서 나타내면 다음과 같다.
즉, 오일러 공식을 통해 좌표 $(x, y)$를 각도 $\theta$만큼 회전시킬 수 있는 것이다.
실제로 $e^{i \theta} \cdot (x+iy)$를 하면 2차원 유클리디언 공간에서 각도 $\theta$만큼 회전한 좌표가 나온다.
오일러 공식에 의해 복소수를 삼각함수로 표현할 수 있다는 점에 착안하여 삼각함수 없이도 회전변환 할 수 있게 해주는 방법. (수정)
오일러 공식을 허수 평면에서 나타내면 다음과 같다.

즉, 오일러 공식을 통해 좌표 $(x, y)$를 각도 $\theta$만큼 회전시킬 수 있는 것이다.
실제로 $e^{i \theta} \cdot (x+iy)$를 하면 2차원 유클리디언 공간에서 각도 $\theta$만큼 회전한 좌표가 나온다.
이때의 실수부와 허수부를 좌표 $(x^{‘}, y^{‘})$라고 할 때, $x^{‘}$와 $y^{‘}$는 다음과 같다.
이것은 내가 알던 회전변환 행렬과 같다. 결론적으로 2차원 유클리디언 평면 위의 한 점을 허수평면에서 나타낸 뒤, $e^{i \theta}$를 곱하여 회전한 좌표를 구하면 회전한 좌표를 구할 수 있다. 더욱 간단하게 말하면
1843년 수학자 William R.Hamilton은 3차원 회전을 표현할 수 있는 복소수의 형태를 발견했다. 그것을 쿼터니안이라고 불렀다. 쿼터니안의 형태는 $q_0+q_{1}i+q_{2}j+q_{3}k$이다.
3차원 유클리디언 공간의 한 점을 pure quaternion의 형태로 나타낸다. 실수부가 없는 쿼터니안을 pure quaternion이라고 하는데, 표현하자면 $q=0+xi+yj+zk$이다. 회전은 $|q_{R}|=1$인 쿼터니안 $q_{R}$로 표현된다. 한 좌표계 A에서 다른 좌표계 B로 회전하는 것은 conjugation operation을 적용한 것이다.
그 결과 $q_{B}$도 pure quaternion으로 표현된다.
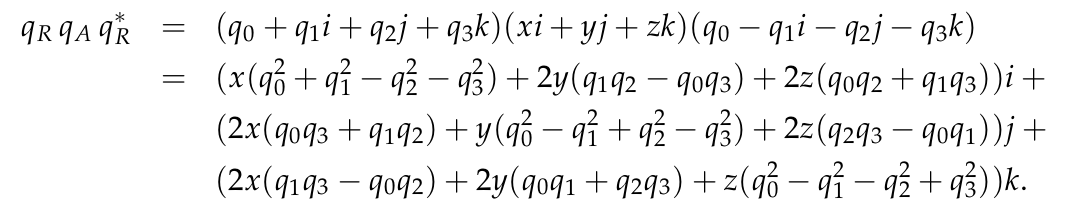
긴 다항식을 풀면 이런 형태로 정리된다. 각각 허수 벡터 $i, j, k$의 허수부로 깔끔하게 정리되고, 다시 허수부 안에서 3차원 유클리디언 공간의 벡터 $x, y, z$의 축으로 정리된다.
이때, 벡터 $i, j, k$와 $x, y, z$를 떼고 남은 회전행렬 $M$은 다음과 같이 표현할 수 있다.
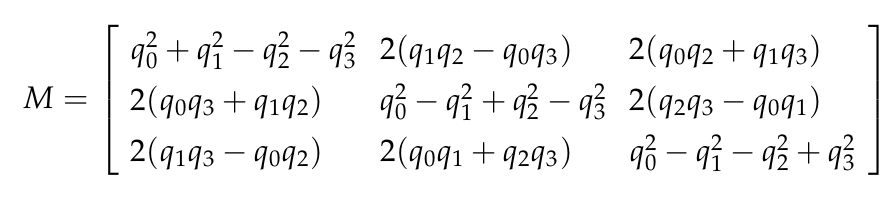
따라서 $q_{R}q_{A}q_{R}^{*}$을 $M$으로 나타내면 다음과 같다.
Matrix $M$은 $|q_{R}|=q_{0}^2+q_{1}^2+q_{2}^2+q_{3}^2=1 \; \leftarrow$ 이 특성때문에 간략하게 표현할 수 있다.
Matrix $M$을 간략하게 표현하면
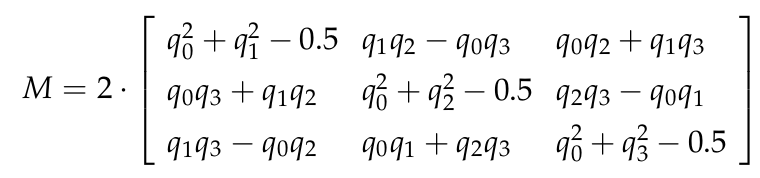
회전행렬 $M$에 $trace$ 함수를 취하면 행렬의 대각합을 구할 수 있다.
이 식으로 $q_{0}$을 구할 수 있다.
$q_{0}$을 알고 있으므로 $M_{11}$로부터 $q_{1}$을 구할 수 있다.
같은 방식으로 $q_2$와 $q_3$도 구할 수 있다.
이로서 $q_0, q_1, q_2, q_3$에 대한 식을 구했다. 이제 오일러 각 회전 행렬이 주어졌을때를 한번 생각해보자. $z$축을 중심으로 $\varphi$만큼 회전한 3차원 회전 행렬은 다음과 같다.
이 회전행렬에서 $Trace(M)=2cos \; \varphi+1$이다. 이를 위에서 구한 식에 대입한다.
그러므로, $z$축을 중심으로 $\varphi$만큼 회전한 쿼터니안은 다음과 같다.
같은 방식으로 $x$축, $y$축을 중심으로 회전한 쿼터니안 역시 구할 수 있다.
쿼터니안을 사용할때 회전이동밖에 안되나요? 평행이동을 같이 표현할 수는 없나요?
그냥 쿼터니안 회전행렬 $M$을 곱해주기 전에 평행이동성분을 추가해주면 됨.
터틀봇의 자세는 위치(3차원 좌표계)+방향(쿼터니안 x,y,z,w)으로 표현
어제 보니까 x,y는 고정, 회전할때 z, w값만 바뀐다. 로봇의 z축이 천장 방향, x축이 전진 방향이었으니 z축 회전이겟지?
뜬금없이 z가 실수부이진 않을테니… $z=sin \; \frac{\varphi}{2}$, $w=cos \; \frac{\varphi}{2}$ 라는 결론이 나온다.
근데 왜 쓰는지 아직도 모르겠네?? 왜지??
Comments